In a series resonance circuit, the resonance condition occurs when the inductive reactance of the circuit becomes equal to the capacitive reactance. In this condition, the circuit current is in phase with applied voltage. The series RLC circuit at resonance is called a series resonance circuit.
A typical series resonance circuit is depicted in the following figure.
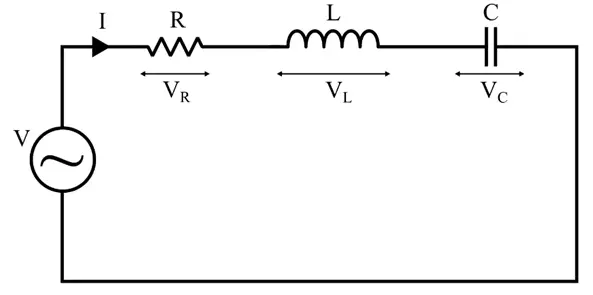
In this circuit, the voltage across the inductor and capacitor is equal, i.e.
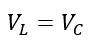
In a series RLC circuit, the resonance occurs at a specific frequency, called resonance frequency (fr). The resonance frequency is a value of the supply frequency at which the inductive reactance becomes equal to the capacitive reactance.
At resonance frequency,
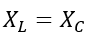
Where XL is the inductive reactance, and XC is the capacitive reactance. At the resonant conditions, the reactance of the inductor and capacitor becomes equal.
The series resonance circuit is widely used in various electronic applications like tuning circuits of radios, TVs, etc.
The voltage equation can be described from the above-given RLC circuit. To obtain the voltage equation of the series RLC circuit, let’s apply KVL to the circuit, we get,
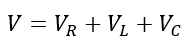
If I is the current flowing through the circuit, then
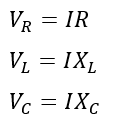
Therefore, the voltage equation can be written as
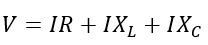
Also, the reactance XL and XC are given by,
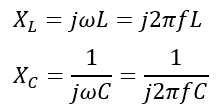
Therefore,
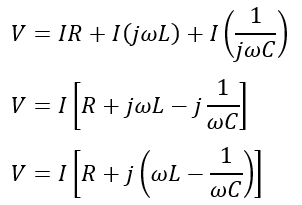
Hence, the above equation is in the form of V = IZ, where Z is called the impedance of the circuit, i.e.
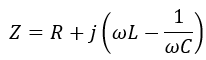
Now, let us analyze the series resonance condition to derive the expressions of different electrical quantities.
Electrical Quantities of Series Resonance Circuit
The subsequent sections illustrate the process of deriving expressions of different electrical quantities at series resonance.
(1). Resonance Frequency at Series Resonance:
The supply frequency at which the inductive reactance and capacitive reactance become equal to each other is called the resonance frequency. It is denoted by fr.
At series resonance,
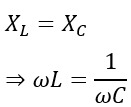
Here, ω = ωr, angular resonance frequency.
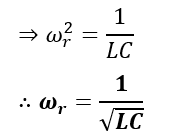
The linear resonance frequency will be,
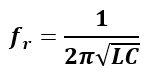
From the above equation, it is clear that the series resonance frequency is independent of resistance.
(2). Impedance of Series Resonance Circuit:
The impedance of a series RLC circuit is given by,
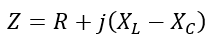
At series resonance,
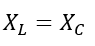
Therefore,
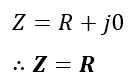
Hence, the impedance of a series resonant circuit is equal to the resistance of the circuit. Therefore, at resonance, a series RLC circuit attains the minimum value of the impedance.
(3). Current through Series Resonance Circuit:
The current through series RLC circuit shown above is given by,
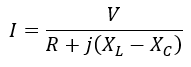
At series resonance, XL = XC, then,
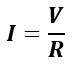
Hence, the circuit draws current from the source only due to the resistance of the circuit. It is the maximum value of the current that can flow through the series RLC circuit.
The figure shows the relation between the series resonance circuit’s current, impedance, and resonance frequency.
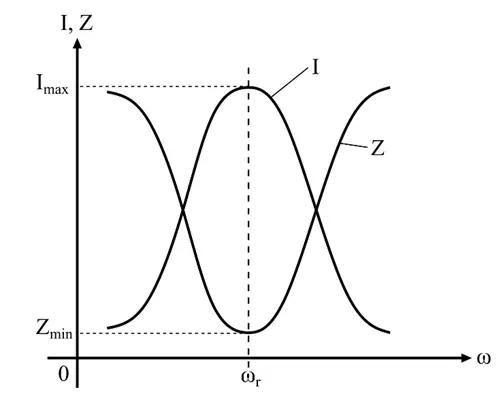
(4). Quality Factor
The quality factor of a series RLC circuit is defined as a ratio of energy stored in each cycle to the energy dissipated in each cycle, i.e.,
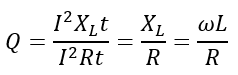
Also,
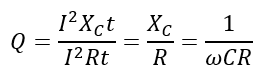
At series resonance,
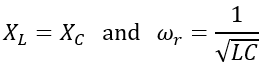
Therefore,
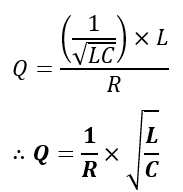
Now, let us consider a numerical example to understand the application of formulas derived in the above sections of this article.
Solved Problem
Numerical Example – A series resonance circuit consisting of a resistor of 50 Ω, a capacitor of 5 µF, and an inductor coil of 30 mH. This series circuit is connected across an AC source of 50 volts RMS voltage. Calculate the resonant frequency of the circuit, current through the circuit at resonance, impedance of the circuit at resonance, and quality factor of the circuit.
Solution – Given data of the circuit are,
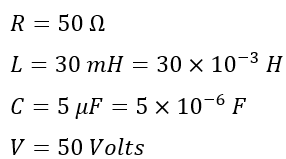
The resonant frequency of the circuit is,
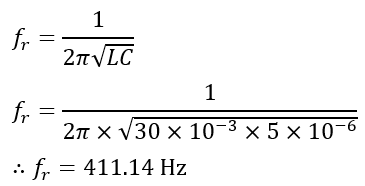
The current through the circuit at resonance is,
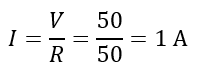
The impedance of the circuit at resonance is,
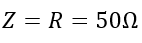
The quality factor of the circuit is;
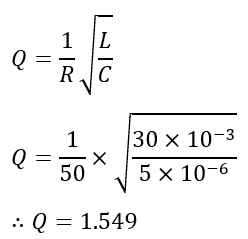
This is all about a series resonance circuit and its various electrical quantities.
