Capacitive reactance is the opposition offered by a capacitor to the flow of electric current through it. The capacitive reactance depends on the frequency.
We use capacitors in AC and DC circuits. The behavior of the capacitor is different for AC and DC. Why? it is because DC frequency is zero and AC frequency has some definite value. The reactance of the capacitor is different in both cases.
When we apply DC voltage to the capacitor, the capacitor draws a charging current & charges up to the supply voltage. On reduction of supply voltage, the capacitor discharges & the voltage across capacitor decreases.
When we apply AC voltage to the capacitor, the voltage across a capacitor is not constant and it goes positive in half cycle, and a negative value in next half cycle. In these conditions, capacitor charges and discharges on a continuous basis depending on the supply frequency.
In a positive half cycle, the capacitor charges, and in the next half-cycle the capacitor feedback the stored energy to the source. Thus, for a complete cycle, the power consumed by the capacitor is zero.
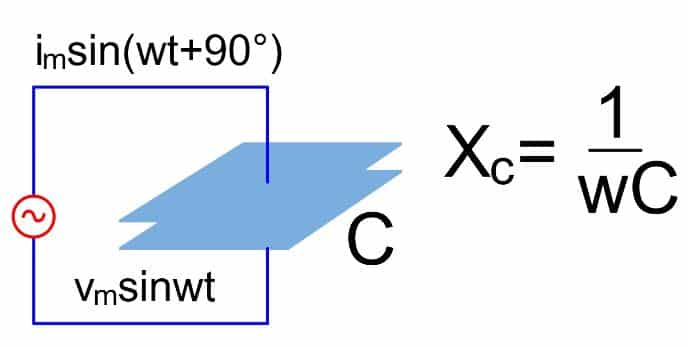
The internal impedance of the capacitor limits the charging and discharging current. This internal impedance is the reactance of the capacitor, and we denote it with the symbol XC. Its unit is Ohm.
How Capacitive Reactance Changes with Frequency?
The resistance of a circuit does not change with frequency. The resistance only changes with changes in the temperature. It is frequency independent. However, the reactance of the capacitor depends on the frequency. Thus, it changes with a change in frequency.
What is the relation between frequency & capacitive reactance?
The capacitive reactance is inversely proportional to the frequency. As a result, the reactance increases with a decrease in frequency. Similarly, the reactance of the capacitor decrease with an increase in frequency.
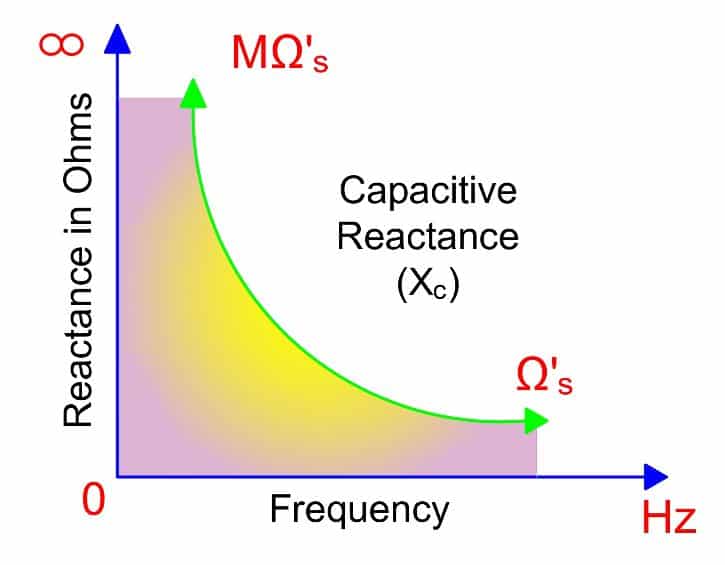
With an increase of frequency, electric charges reach from one plate to other more rapidly. Therefore, the reactance of the capacitor decreases with an increase in frequency.
Thus, the reactance is frequency-dependent.
Formula of Capacitive Reactance
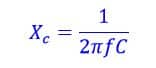
| Where, | |
| XC | Capacitive Reactance in Ohms( Ω ) |
| f | Frequency in Hertz (Hz) |
| C | Capacitance in Farad (F) |
Capacitive Reactance against Frequency and Capacitor Current
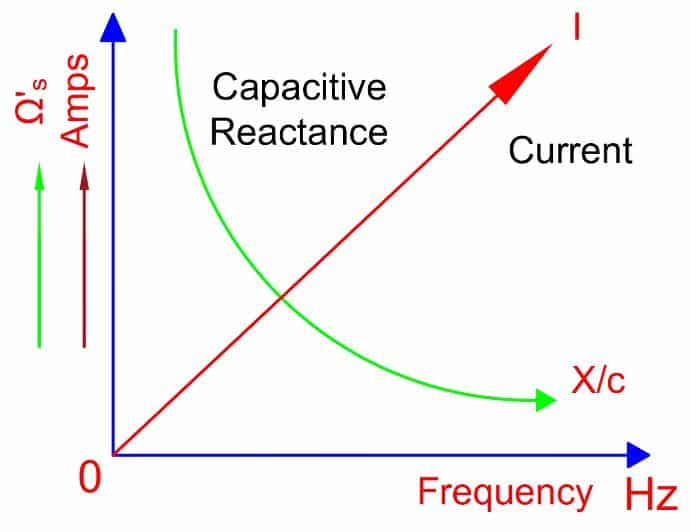
The reactance of capacitor of the capacitor is inversely proportional to the frequency. The relationship between capacitive reactance and frequency is as shown below.
Solved Problems on Capacitive Reactance
Problem No.1
Calculate the reactance of capacitor value of a 110nF capacitor at a frequency of 5kHz and again at a frequency of 10kHz.
Capacitance Value = 110 nF = 110 X 10-9 Farad
XC at 5 KHz
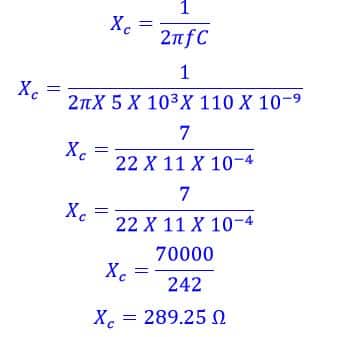
XC at 10 KHz
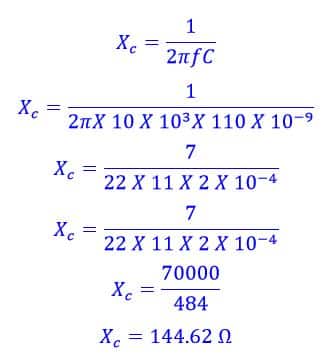
Problem No2
At what frequency a 2 uF Capacitor have a reactance value of 100Ω?
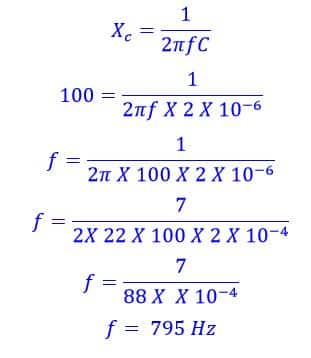
Problem No3
Calculate the value of a capacitor in farads when it has a reactance of 100Ω and is connected to a 50Hz supply.
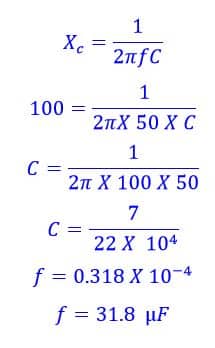
From the above examples, it is clear that the reactance of the capacitor varies when connected to a variable frequency supply. Thus, The capacitor acts as a frequency-controlled variable resistor in this case.
At very high frequencies such as 1Mhz, the capacitor has a low reactance value, and the capacitor acts like a short circuit. Therefore, at a steady state, the DC capacitor has infinite reactance, and the capacitor acts like an open circuit.
Read Next: