A person “A” can dig 2 feet of soil in one hour. Another person “B” can dig 2 feet of soil in two hours. Who has more power? Definitely, person A has more power than person B because person A is doing the same work half of the time. Thus, we can define power as the rate of doing work. The faster the rate of doing work, the more is the power.
The rate of doing work is not constant in the case of people engaged in doing the work. The rate of doing work decreases with time because the man gets exhausted with time. Therefore, we consider the average power concept in such cases. Yes, the machine can deliver constant power. A 50 KW motor can deliver the constant load to drive the mechanical load or we can say the motor is the constant power machine. Now, we can easily define what power and average power are.
What is Power?
Power is the rate of doing work or activity. The more the power, the more the amount of work. A powerful car accelerates fast and covers a distance of 100 meters in 5 seconds. The other less powerful car accelerates and covers the same distance of 100 meters in 15 seconds. It means the powerful car does more work than a less powerful car.
Solved Example
Water pumps A and B deliver 100 kg of water at a 50-meter height. Pumps A and B discharge 100 kg of water in 5 and 10 minutes, respectively. Which pump has higher power?
Work done = mgh
W = 100 X 9.8 x 50 =49,000 Joules
P = Work done/ Time
Power (Pump-A) = 49000/(5X60) = 49000/300 =163 J/Sec.= 163 Watts [ 1 J/s = 1 watt ]
Power (Pump-B) = 49000/(10 x60) = 49000/600 = 81.5 J/sec = 81.5 Watts
Pump A is more powerful than pump B.
Power Formula
Power is the rate of doing work. The power is proportional to the work done,
Power ∝ Work done ——–(1)
and power is inversely proportional to the time taken for doing the work.
Power ∝ 1/ Time taken ——-(2)
Therefore,
Power ∝ Work done/ Time taken —–(3)
The formula of power is given below.

Unit of Power
SI Unit of work is Joule and the SI unit of time is second. Therefore, the SI unit of power is Joule/ second. 1 Joule/Second is 1 Watt.
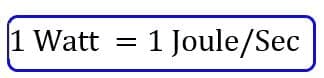
The abbreviation of Watt is W. Another unit of power is Horsepower.
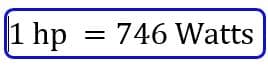
Other Units of Power
| Units | Abbreviation | Equivalent Watt Unit |
| Kilowatts | kW | 1 x 103 W |
| Megawatts | MW | 1 x 106 W |
| Gigawatts | GW | 1 x 109 W |
| decibel-milliwatts | dBm | 30dBm = 1 watt |
| British Thermal Unit | BTU | 3.412142 BTU/hr = 1 w |
| Calories per Second | Cal/sec | 0.24 calories per second cal/sec = 1 W |
What is Average Power?
When the rate of doing work is different for different intervals, then the average power is the ratio of the total amount of work done in the total amount of time.
For example, A person has to carry 10 kg weight from ground level to 50 meters height in a multi-story building. Up to 10 meters, he takes 60 seconds; 10 meters to 30 meters, he takes 4 minutes, and for the rest 20 meters, he takes 8 minutes. Then, we can calculate the average power as follows.
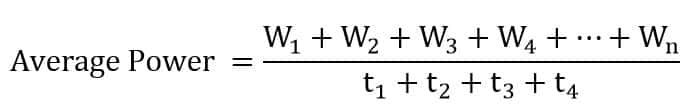
Work done
Total work done(W) = W1+W2 +W3
= mgh1 + mgh2 + mgh3 = (10 x 10 x10) + (10 x 10 x 20) + (10 x10 x20)
W= 1000 + 2000 + 2000 = 5000 J
Time taken to complete the task
Total time taken = t1+ t2+ t3 =60 + 4 x60 + 8 x60= 60 +240 +480 = 780 seconds
Average power = Total work done / Time taken
=5000/780 =6.4 J/s = 6.4 Watts
Dimension of Power
Work (W) = Force X displacement = Mass X acceleration(meter/sec 2) X displacement
Work (W) = M x L/T2 x L = M0L2T-2
Power = Work/ Time = M0L2T-2 / T = M0L2T-3
The dimensional formula of power is M0L2T-3
Electric Power
Electric power is the rate of transferring electrical energy of moving charges to some other forms of energy like heat, chemical, or mechanical energy. The alternator generates the electric power. The other power generation sources are wind turbines, hydro generators, and solar systems.
Electric Power Formula
| P = VI = I2 R = V2/R |
Where- V, I, and R is voltage, current, and resistance, respectively.
Solved Example
A 100-watt A bulb is switched on 24 hours a day, and another 100-watt B bulb is turned on for only 12 hours. Find the energy consumed by both the bulbs in one day.
Solution:
Both A and B bulbs remain ON for 12 hours;
Power = 100+ 100 = 200 watts
Energy = Power x Time
= 200 x 12 = 2400 Watts
= 2.4 kWh (kilowatt-hour)
Now, for the next 06 hours, only bulb A remains ON hence,
Power = 100 watts
Energy = 100 x 12 = 1200 Watts =1.2 kW h
Average Power = Total energy consumed(kWh) / Total time taken(h)
= (2.4 + 1.2) /24
= 0.15 kW
Read More: