Electric Power Definition
The rate at which work is done is called an electric power. An electrical source has electrical charges stored in it. Therefore, the rate of transfer of electrical charges is electrical power. Thus, the higher the transfer rate of the charges, the more the power of the source. In other words, the rate of transfer of electrical charge converts electrical energy into other forms of energy. The unit of electric power is the watts.
For example, a heater receives electrical energy and converts it into heat energy. The AC generator or alternator generates the electrical power. The power is then transferred to a distant location for its utilization.
Electric Power Formula
The formula of electrical power is given by
| P = Work done/ Time = Energy/ Time = VIt/t = VI |
| P= VI |
Where,
P = Power
V = Potential Difference in the circuit
I = Current in the circuit
We know, according to Ohm’s law, V= IR
Where,
V= Potential difference in the circuit
I= Circuit Current
R = Resistance in the circuit
The other form of electrical power formulas are given by
| P = I2R |
| P = V2/R |
Units of Electrical Power
The unit of electrical power is the watts.
If a potential difference of 1 volt is across an electrical circuit, and the circuit draws 1-ampere current, then the power consumed by the circuit is 1 watt.
P = VI
If, V = 1 Volt, I = 1 Ampere, P= 1 Watt
The bigger units of power are kilowatts (kW), gigawatts (GW), and megawatts (MW).
There are two types of electrical power
- DC Power
- AC Power
1. DC Power
The current flows in the same direction as the applied DC voltage. Therefore, power is equal to the product of voltage and current. The DC generator, fuel cell, and battery produce DC power.
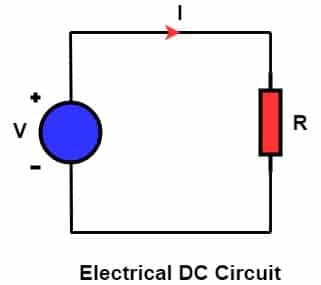
| P=VI |
P = Power in Watt
V= Voltage in Volts
I = Current in amperes
2. AC Power
The current in the AC circuit does not remain in the phase with the voltage. Yes, the current and voltage in the AC circuit are in phase for the pure resistive circuit. We classify AC power into three categories. These are active power, reactive power, and apparent power.
1. Active Power
The active power (P) is the real power consumed by an electrical circuit. The current in the circuit is in phase with the voltage. The active power in the AC circuit is given by
P = Vrms Irms CosΦ
Where,
P – the real power in watts.
Vrms – RMS voltage
Irms – RMS current
Φ – Phase angle between voltage and current.
2. Reactive Power
Reactive power (Q) is the watt-less power. We measure reactive power in volt-ampere reactive. The circuit draws a reactive current. If the load is inductive or capacitive, the current is out of phase with the applied voltage. The reactive power in the AC circuit is given by
Q = Vrms Irms SinΦ
Where,
P – the real power in watts.
Vrms – RMS voltage
Irms – RMS current
Φ – Phase angle between voltage and current.
3. Apparent Power
Apparent power (S) is the vector sum of the active and reactive power. The relationship between active, reactive, and apparent power is given below.
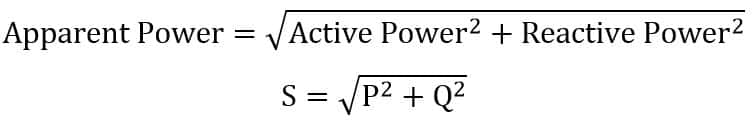
Solved Problems on Electric Power
Q. 1 A 220 Volts heater draws 4-ampere current from the power source. What is the electric power consumed by the heater?
P= VI = 220 x 4 = 880 Watts
Q. 2 Calculate the electrical power of an electrical circuit consisting of resistance 4 Ω and a circuit current of 5 A.
R = 4 Ω
I = 5 A
P = I2R = 5 x 5 x 4 = 100 Watts
Q. 3 Calculate the electric power of an electrical circuit consisting of resistance 4 Ω and voltage applied is 220 volts.
R = 4 Ω
I = 220 A
P = V2/R = 220 x 220 / 4 = 12.1 kW