This article aims to define active, reactive, and apparent power & their importance in an electrical circuit.
Active Power
Definition: The power which is actually consumed or utilized in an AC Circuit is called True power or Active power or Real power. It is measured in kilowatts (kW) or MW. It is the actual outcomes of the electrical system which runs the electric circuits or load.
Reactive Power
Definition: The power which is not consumed or utilized in an AC Circuit is called reactive power. It is basically watt-less power. The reactive power draws the current from the source but does not consume power. It is measured in VA or kVA.
Apparent Power
Definition: The power which flows back and forth which means it moves in both directions in the circuit or reacts upon it, is called Reactive Power. The reactive power is measured in kilovolt-ampere reactive (kVAR) or MVAR.
It has been seen that power is consumed only in resistance. A pure inductor and a pure capacitor do not consume any power since in a half cycle whatever power is received from the source by these components, the same power is returned to the source. This power which returns and flows in both directions in the circuit is called Reactive power. This reactive power does not perform any useful work in the circuit.
In a purely resistive circuit, the current is in phase with the applied voltage, whereas in a purely inductive and capacitive circuit the current is 90 degrees out of phase, i.e., if the inductive load is connected in the circuit the current lags voltage by 90 degrees and if the capacitive load is connected the current leads the voltage by 90 degrees.
Hence, from all the above discussion, it is concluded that the current in phase with the voltage produces true or active power, whereas, the current 90 degrees out of phase with the voltage contributes to reactive power in the circuit.
Therefore,
- True power = voltage x current in phase with the voltage
- Reactive power = voltage x current out of phase with the voltage
The phasor diagram for an inductive circuit is shown below:
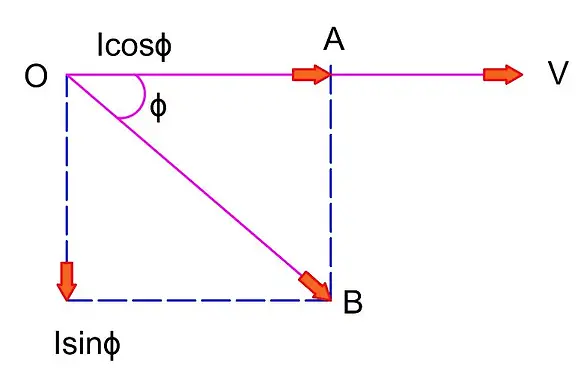
Taking voltage V as a reference, the current I lags behind the voltage V by an angle ϕ. The current I is divided into two components:
- I Cos ϕ in phase with the voltage V
- I Sin ϕ which is 90 degrees out of phase with the voltage V
Therefore, the following expression shown below gives the active, reactive, and apparent power respectively.
- Active power P = V x I cosϕ = V I cosϕ
- Reactive power Pr or Q = V x I sinϕ = V I sinϕ
- Apparent power Pa or S = V x I = VI
Active component of the current
The current component, which is in phase with the circuit voltage and contributes to the active or true power of the circuit, is called an active component or watt-full component, or in-phase component of the current.
Reactive component of the current
The current component, which is in quadrature or 90 degrees out of phase with the circuit voltage and contributes to the reactive power of the circuit, is called a reactive component of the current.