In modern electrical systems, especially with non-linear loads, accurate measurement of AC signals is critical. This is where True RMS measurement outperforms traditional methods.
Unlike average responding meters, a True RMS meter accurately measures both sinusoidal and distorted waveforms—ensuring precise results even with harmonic-rich signals.
In this article, we’ll explore the True RMS formula, the working principle of True RMS meters, and the difference between RMS and True RMS to help you choose the right instrument for accurate voltage and current measurements.
What is True RMS? Meaning & Working
True RMS measurement is more reliable and accurate than RMS measurement. We express the AC voltage and current in its effective or RMS value.
RMS value = Square root of the average of the square of AC current or voltage over a period.
The meaning of True RMS lies in its ability to measure both pure and distorted AC waveforms accurately.
The RMS measurement is accurate only if the waveform is perfectly sinusoidal.
However, nowadays, most loads are non-linear, and the voltage or current waveform is often distorted. In this case, true RMS measurement is most suitable.
Note: RMS meters typically measure the peak value, then calculate the RMS.
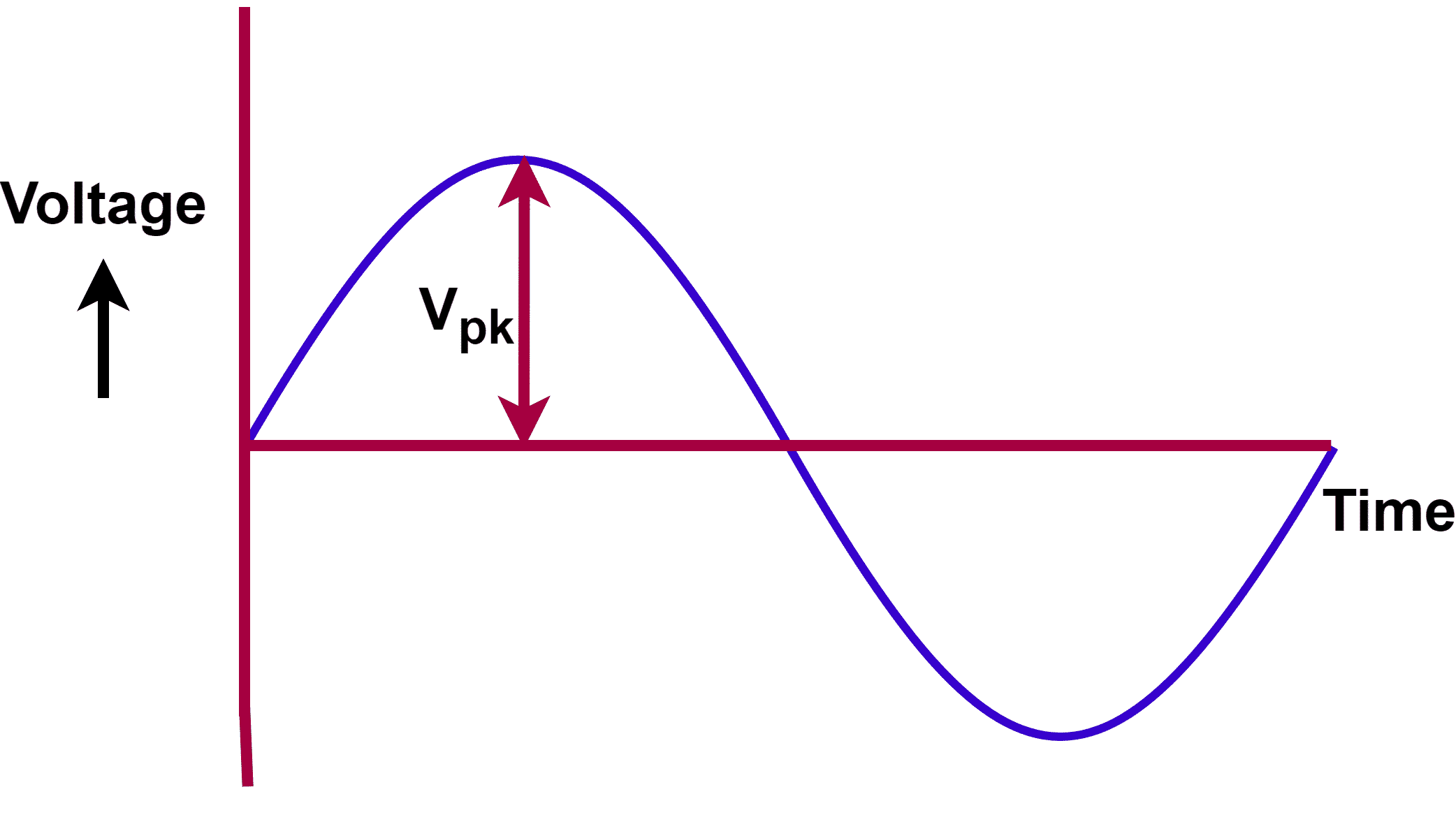
The formula of the RMS value of sinusoidal voltage is given below.

Let’s understand why the True RMS meter is more accurate, and why the average responding or RMS measuring meter may produce errors.
RMS vs True RMS: What’s the Difference?
Understanding the difference between RMS and True RMS is essential for selecting the right measuring instrument.
The meter that uses the averaging technique to calculate the RMS value of voltage or current is called an RMS measurement. The RMS value of the AC current or voltage has the ssame heating effect as the DC of the same magnitude.
We express the alternating voltage or current for its effective values. The square root of the average square of alternating voltage or current is called the RMS value.
The ratio of RMS to the average value for a perfectly sinusoidal waveform is 1.11.
RMS value = 1.11 × Average value
For a perfect sinusoidal voltage waveform:
Peak value = 1.414 × RMS
RMS = 0.707 × Peak value
Thus, the average responding meter gives the RMS measurement correctly for a pure sinusoidal waveform.
However, the measurement’s accuracy depends on the perfection of the sinusoidal waveform.
Measuring distorted waveform with an RMS meter will produce an enormous error.
The true RMS (TRMS) meter calculates the heating effect of the waveform by sampling. With a high sampling rate and multiple samples per waveform, the true RMS meter is the most accurate for measuring distorted current/voltage waveforms.
Why is True RMS More Accurate?
The meter uses a more complex mathematical formula for calculating the RMS value.
Therefore, the meter takes more samples per cycle to get the exact value.
True RMS meter working principle: A True RMS meter works on the principle of waveform sampling and integration to calculate the exact heating effect.
True RMS Formula
The formula for True RMS is crucial in calculating the effective value for both sinusoidal and non-sinusoidal waveforms.

True RMS Responding Voltmeter
A True RMS responding voltmeter accurately measures AC voltage regardless of the waveform shape. Unlike average responding meters, which assume a sine wave, these voltmeters analyze the actual waveform using advanced sampling and digital integration.
This allows them to measure:
- Non-sinusoidal waveforms like square, triangular, or pulse-width modulated signals.
- Distorted signals from electronic devices such as VFDs or DC drives.
These meters work by:
- Sampling multiple points in a waveform,
- Squaring each sample,
- Averaging them, and
- Taking the square root to find the effective (RMS) value.
How to Calculate True RMS Value
For example, the True RMS voltage of the window size of 100 is equal to the square root of each voltage of the 100 instantaneous voltages squared divided by 100.
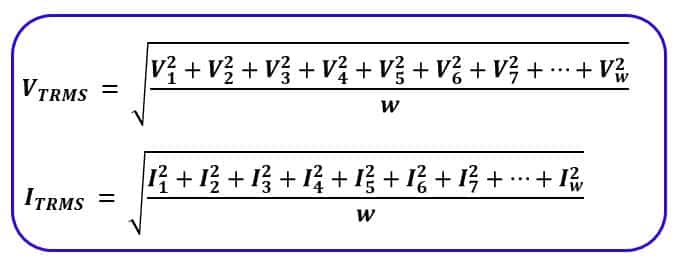
Example:
Suppose we have 5 instantaneous voltage samples taken equally spaced in time:
V = [4V, 5V, 6V, 5V, 4V]
To calculate the True RMS voltage:
True RMS = √[(V₁² + V₂² + V₃² + … + Vₙ²) / n]
True RMS = √[(4² + 5² + 6² + 5² + 4²) / 5]
= √[(16 + 25 + 36 + 25 + 16) / 5]
= √[118 / 5]
= √23.6
≈ 4.86V
So, the True RMS voltage is approximately 4.86V.
The more the number of samples, the more accurate the measurement. The meter accounts for current spikes, noise, and distortion, therefore it gives the correct measurement.
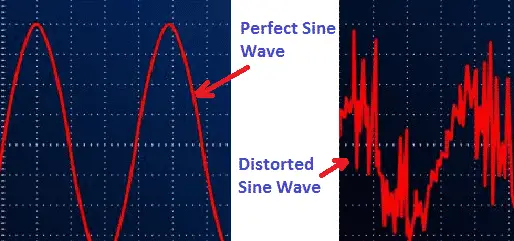
Sinusoidal vs Non-Sinusoidal Waveform – True RMS Accuracy
Measuring Linear Loads with RMS and True RMS Meters
The average responding meter can measure the voltage and current. The average responding meters give accurate readings for linear loads.
The linear loads are heaters, induction motors, and incandescent lamps. The linear load draws current in phase with the applied voltage.
Therefore, the current drawn by non-linear loads increases in proportion to the voltage. In other words, the current drawn by linear loads is sinusoidal.
In the case of linear loads, both true RMS and average responding meter can be used to measure voltage or current.
Why True RMS Is Essential for Non-Linear Load Measurement
The average responding meter reads low. We use a true RMS meter to read the current of non-linear loads.
The non-linear loads are the DC Drive, variable frequency drive, and electronic equipment. Semiconductor devices like a diode, SCR, and IGBT have non-linear characteristics.
The current drawn by these devices is not linear to the applied voltage, and because of this, the current waveform is distorted.
The semiconductor devices produce harmonic current in the electrical network. The average responding meter can not measure the non-sinusoidal current accurately.
Therefore, non-linear loads need a True RMS meter for measuring current and voltage.
If the meter is labeled and specified to respond to the True RMS value of the current, it means the meter’s internal circuit calculates the heating value of the current or voltage. This method gives accurate measurement irrespective of the current wave shape.
The True RMS meter reads correctly for all types of wave shapes, whether sine waves, square waves, triangular waves, etc.
If we use the average responding meter, the reading errors of different wave shapes are given below.
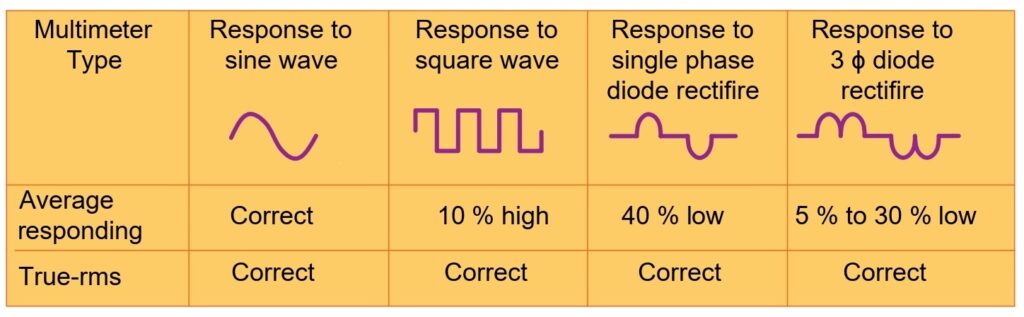
Where Should You Use a True RMS Meter?
If the voltage or current waveform is perfectly sinusoidal, the True RMS and average responding meter read accurately.
In recent years, non-sinusoidal current devices have been popularly used. The recently developed devices are as follows:
- Variable frequency drives(VFDs)
- DC drives
- Electronic ballast
- HVAC
- Solid-state contactors
In these devices, the current flows in spikes rather than having a perfect sinusoidal waveform.
The current wave shapes have a dramatic effect on the measurement. If an average responding meter is used, then there will be an appreciable amount of measurement error.
True RMS instruments are much more accurate than RMS instruments when measuring distorted waveforms or waveforms deviating from sinusoidal waveshapes..
True RMS Multimeter Specifications
A True RMS multimeter means it can accurately measure AC values regardless of wave distortion. Here are the Technical Specifications of a 4½ Digit True RMS Multimeter:
| Parameter | Specification |
|---|---|
| DC Voltage Range | 200mV / 2V / 200V / 1000V |
| DC Voltage Accuracy | ±(1.0% + 5) |
| AC Voltage Range | 2V / 20V / 200V / 750V |
| AC Voltage Accuracy | ±(0.8% + 25) |
| DC Current Range | 200µA / 2mA / 200mA / 20A |
| DC Current Accuracy | ±(0.5% + 4) |
| AC Current Range | 200mA / 20A |
| Resistance Range | 200Ω / 2kΩ / 20kΩ / 200kΩ / 2MΩ / 20MΩ |
| Resistance Accuracy | ±(0.4% + 5) |
| Capacitance Range | 2nF / 2µF / 200µF |
| Capacitance Accuracy | ±(4.5% + 50) |
| Conductance Range | 0.1 ~ 100 nS |
| Conductance Accuracy | ±(1.0% + 30) |
| Frequency Range | 20kHz / 200kHz |
| Frequency Accuracy | ±(1.5% + 25) |
| Input Impedance | 10MΩ |
| Sampling Rate | 2 times/sec |
| AC Frequency Response | 40Hz – 400Hz |
| Max. Display | 19999 |
| Other Features |
Full function protection, anti-high voltage circuit Low battery indication Continuity buzzer Auto power off |
Conclusion
True RMS measurement ensures accuracy in AC signal reading—especially when the waveform is distorted. Whether you’re dealing with VFDs, electronic ballasts, or non-linear loads, using a True RMS meter is essential for correct current and voltage values.
Understanding its formula, working principle, and differences from conventional RMS meters will help you select the right tool for your measurement needs.
Related Articles: