Peak Value
The sinusoidal waveform starts from zero, attains peak value, and again comes down to zero in a positive half cycle. In the next negative half cycle, the waveform goes through a negative peak value and comes down to zero value. Thus, in one complete cycle, the waveform attains a positive peak value at 90 degrees and a negative peak value at 270 degrees.
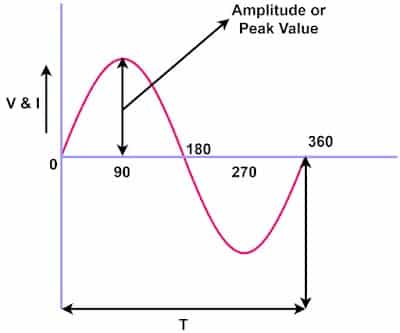
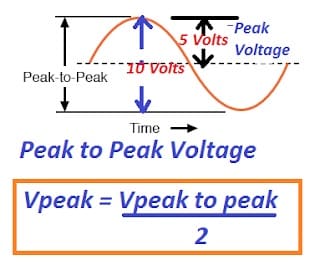
The maximum value attained by an alternating waveform during one cycle is known as its peak value. The peak value is also termed the crest value. The peak value of symmetrical alternating voltage and current waveform can also be determined by measuring the peak-to-peak value of the waveform.
Average Value
The sinusoidal waveform has a different magnitude of voltage or current at the different instants of the waveform. The magnitude of the current or voltage at a particular instant is called the instantaneous value of the waveform. The average of all the instantaneous values of an alternating voltage and current over one complete cycle is known as an average value.
For the symmetrical sinusoidal waveform, the positive half cycle is symmetrical to the negative half cycle. Therefore, the average value of one complete cycle is zero. However, the average value is calculated without considering the signs. Therefore, only a positive half cycle is considered for determining the average value of the alternating waveform.
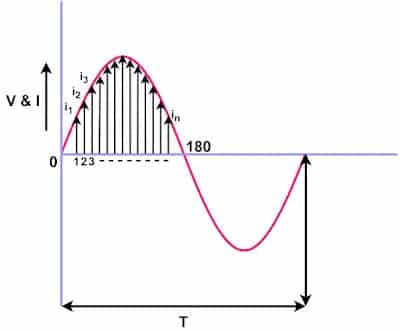
In the above diagram, Let i1, i2, i3…….. in be the mid ordinates.
The average value(Iav) of the sinusoidal waveform,
= Mean Value of the mid-ordinates
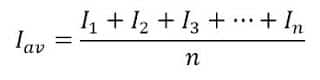
Formula Derivation of Average Value of Sinusoidal Waveform
The average value of the sinusoidal waveform is obtained by adding instantaneous values of voltage or current over one-half cycle only.
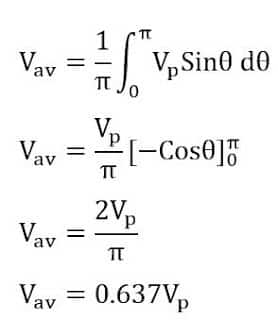
The peak value of the sinusoidal voltage is 300 volts, and the average value will be;
Vav = 0.637 x 300
Vav =191.1 Volts
RMS Value
The ‘RMS Value’ stands for Root Mean Squared value. The RMS value of an alternating current is given by that steady (D.C) current, which, when flowing through a given time, produces the same amount of heat as produced by the A.C when flowing through the same circuit for the same time. It is also known as the effective value of A.C.
DC Value Equivalent of RMS Value
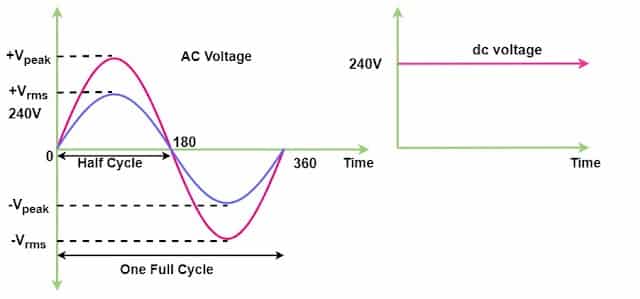
In the above diagram, if we calculate the amount of heat produced with the flow of electric current through the same circuit for the same time, the AC current, which produces the same heat in the circuit as heat produced by DC, is called the RMS value of AC. The RMS value is 240 VAC, which means that the 240 VAC produced the same heat as the 240 Volts DC voltage for the same circuit.
The RMS value can be determined using the following methods.
Graphical Method
The graphical method is used to find the RMS value of any non-sinusoidal time-varying waveform. If the waveform is symmetrical about the axis, the analytical method can be used. In the graphical method, a number of mid-ordinates are taken, and their instantaneous value is recorded.
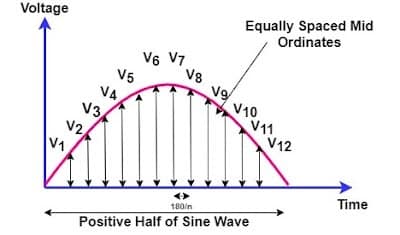
Each mid-ordinate value of a waveform is multiplied by itself and added to the next. The squared value is divided by the number of mid-ordinates, and then the square root of the expression gives the RMS value. The accuracy of the measurement depends on the number of midordinates taken to get instantaneous values.

Let the peak value of AC voltage be 25 volts, and the instantaneous value at mid-ordinates of half-cycle of AC are as follows.

The RMS value of the AC voltage is calculated as follows.

The RMS value of the AC wave is 17.68 volts.
Analytical Method of RMS Value Calculation
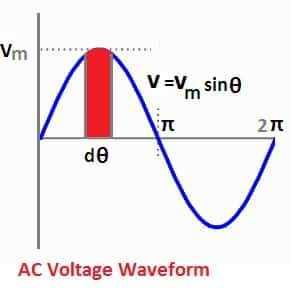
For symmetrical sinusoidal voltage or current waveform, an analytical method can be used to find out the RMS value.
Formula Derivation of RMS Value of Sinusoidal Waveform
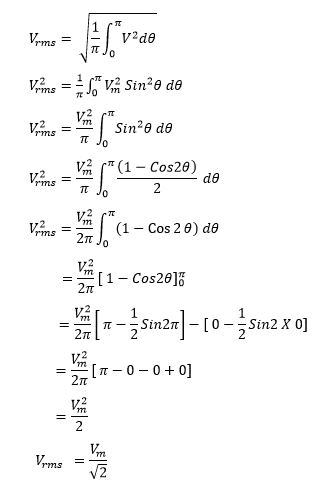
If the peak value of AC voltage is 25 volts, its RMS value will be;
Vrms = 25/1.414 = 17.68 Volts
RMS Voltage Equations
Vrms = 0.707 Vm
Vrms = 1.11 Vavg
The ratio of the RMS value and the average value of the pure sinusoidal waveform is equal to 1.11. If the RMS to average value ratio is other than 1.11, the waveform is said to be distorted.
2 thoughts on “What is Peak Value, Average Value and RMS Value?”