A Sinusoidal wave in the context of Electrical or Electronics Engineering is used to represent a time-varying voltage or current whose average value in a cycle is zero. Mathematically, this waveform can be represented by the equation.
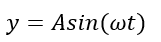
Where y denotes the instantaneous value of voltage or current while A denotes the Amplitude, which is the peak value of the voltage or current. ‘t’ is the instant at which the instantaneous voltage or current is measured, while ‘ω‘ is the angular frequency.
Why Sinusoidal Wave…?
The supply power has Alternating Voltage and Current, so their average value over a cycle is zero. This means the area covered by the voltage/current Vs. time graph in the positive half-cycle is equal to that in the negative half-cycle. This is best represented in a pure form by a sinusoidal waveform. A sine wave is a geometric waveform that periodically oscillates and moves up, down, or side-to-side.
Another importance of the sinusoidal waveform is that it is easy to represent time-varying source power using this waveform as well as the sinusoid function. This is because the rotating generators that generate the power naturally give sinusoidal output if plotted with respect to time by taking the projections.
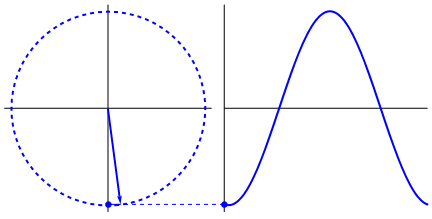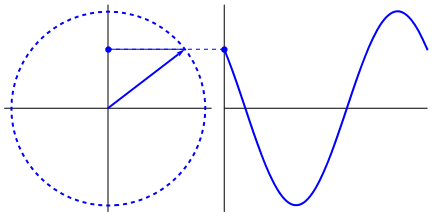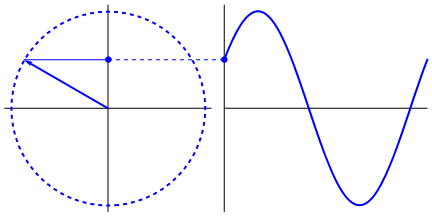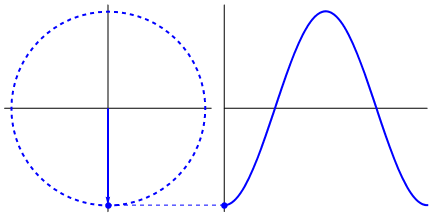
Any other waveform may represent the transmitted power over time, for example, a square wave. But that will not represent the true power output in the purest form as it will have a DC component, which is not present in an AC-generating source. In addition to that, the analysis is complex for not only square waves but any other waveform except sinusoidal, as the Harmonic component of the power gets added to these waveforms.
A sinusoidal wave does not contain harmonic content, and it is the purest waveform. Therefore, when used to transfer power, it results in the lowest losses. Fourier analysis and empirical data confirm this.
Sinusoidal signals are well-suited for frequency domain analysis. Frequency domain analysis is important to study the behavior of a system across different frequencies for the identification of resonances, frequency response characteristics, and the effects of filtering and modulation.
All these points gloss over the importance of a sinusoidal waveform for the representation of a time-varying voltage or current as generated by a power generator.
Fundamentals of a Sinusoidal wave
Now that we have understood the importance of a sine wave equation for representing a time-varying voltage or current, it is important to look at the fundamentals of a sinusoidal waveform in power engineering. Following are the fundamentals of a sine-wave in power engineering.
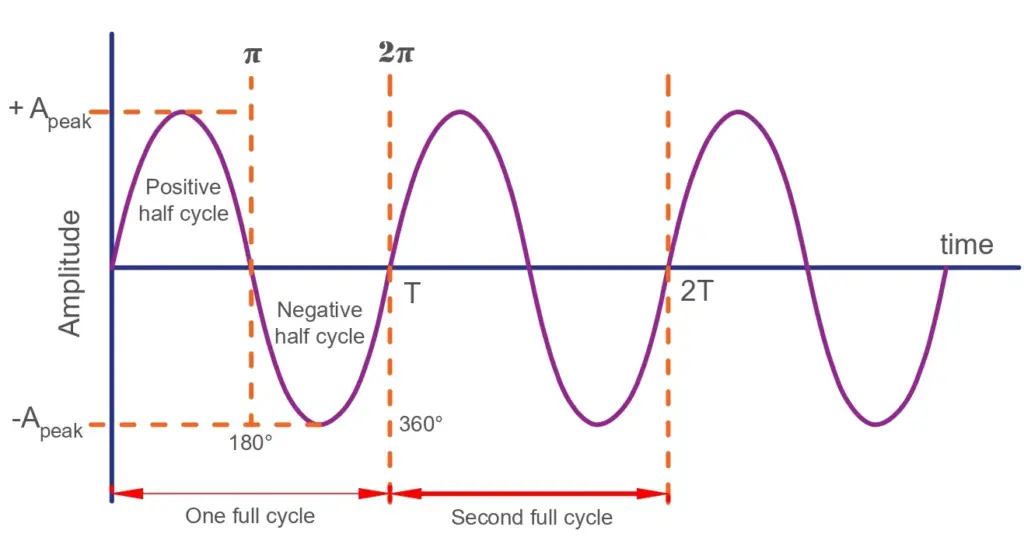
Definition and shape:
As discussed earlier, a sine wave is a periodic waveform oscillating between a positive and a negative maximum value symmetrically with respect to a central axis representing the value zero for the voltage or the current. The area swept by the positive and the negative half of the waveform with respect to time is equal and opposite in a cycle.
Thus, the average value of the time-varying voltage or current over a cycle is zero. The waveform can be mathematically represented as a simple sine function with a certain amplitude, phase, and frequency. The equation for a time-varying AC voltage is given as
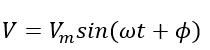
Where V is the instantaneous value of the AC voltage, Vm is the peak value or the amplitude, ω is the angular frequency, t is the time or instant at which the voltage is calculated, and Φ is the phase angle of the voltage.
Maximum Amplitude or Peak Value:
As the name says, it is the peak or maximum value of a cycle’s alternating voltage or current. As evident from the sine-waveform shown above, there are two peak values for an AC voltage or current – one in each half-positive and negative cycle. Once the alternating parameter reaches this peak point, it starts reversing its direction and touches the zero value axis, followed by movement towards the other half.
Any calculation related to insulation and capacity of the power system is done based on this peak value, as the system should be safe and sound to handle the peak voltage or current. The peak or the amplitude is achieved at an angle of 90 degrees and 270 degrees, where the sine function gives the maximum value in the positive and negative half, respectively. It can be shown as follows.
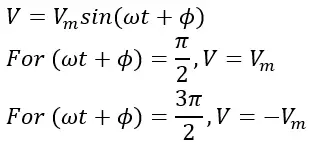
Frequency of Sinusoidal Wave :
The number of cycles completed by the sinusoidal waveform in a second is known as the frequency of the wave. Frequency is calculated in Hertz (Hz). So, a 50Hz voltage or current waveform means that the sine wave completes 50 cycles in a second. Frequency is a function of the speed of the power generator.
The higher the speed of the generator, the higher will be the generated frequency. In electronic systems, however, the frequency of a signal can be changed using frequency modulators.
The following relationship gives the correlation between the frequency of the generated power and the generator speed.
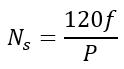
Where Ns is the speed of the alternator, f is the frequency of the power generated, and P is the number of poles of the generated. The sine-wave equation represents the angular frequency and is given as;
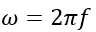
AC impedances like inductive and capacitive reactance depend on the value of the supply frequency. Inductive reactance in a circuit increases with the increase in frequency, whereas capacitive reactance decreases as the frequency increases.
In addition, various phenomena like skin effect, corona loss, Hysteresis loss, and eddy current loss are directly dependent on the power frequency. Thus, it is a fundamental parameter to look at while analyzing a power waveform.
Time Period:
The time period of a waveform is defined as the time taken by the waveform to complete one cycle. The frequency(f) of the waveform tells us about the number of cycles completed in a second. So, the waveform completes f cycles in one second or 1 cycle in 1/f second(s), known as the waveform’s time period. Thus, the time period is technically the reciprocal of the frequency.
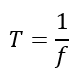
In electronic systems, the speed of the microprocessor is represented using frequencies ranging from a few kHz to MHz, which tells us about the time period or the time of operation of the processor.
Phase Angle:
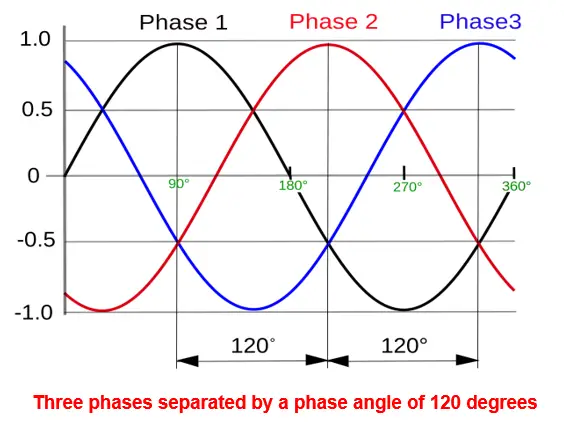
The phase angle tells us about the position of the sinusoidal wave with respect to a reference point in time. It is denoted by the Greek letter ‘Φ’. It is measured in degrees or radians. Phase angle holds significance in the case of a poly-phase supply like a three-phase supply where each phase is 120 degrees phase apart from each other. Phase angle denotes the shift of a particular sine wave horizontally along the time axis.
RMS Value:
RMS stands for Root-Mean-Square. RMS value is calculated by taking the square root of the mean of squared instantaneous voltage or current values in a cycle. RMS value is calculated to analyze a power waveform’s heating or power-producing capability accurately. For a sine wave, it is approximately equal to 0.707 times the peak value.
The relation between RMS voltage and maximum voltage is given as (holds true for current as well).
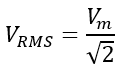
Thus, we can see that the sine wave is one of the most important periodic waveforms. Fourier analysis shows that it forms all other periodic waveforms and is central to all signals and signal processing.
The sine wave can be observed in many areas of science and everyday life because it forms the basis of many oscillating systems, and, like in electronics, using Fourier analysis, these waveforms can be analyzed like a lot of sine waves acting together.
Sinusoidal Waveform Example
If a sine wave is represented as v= 200 sin (314t), then find its RMS value, frequency, and instantaneous velocity of the waveform after 6 ms of time.
Solution:
The sinusoidal wave equation is;
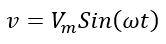

The maximum or peak voltage Vm= 200 volts and,
Angular frequency ω= 314 rad/sec.
The RMS voltage of Sinusoidal wave
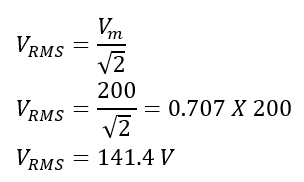
The frequency of sine wave
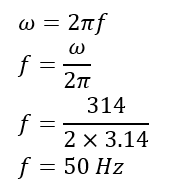
The instantaneous value after a time of 6 ms
