Harmonics and Harmonic Frequency in AC Circuits

Last Updated on October 31, 2021 by Electricalvolt

There are two types of circuit.

1. Linear Circuit

2. Non Linear circuit

In a linear circuit the current follows the voltage.The current increase or decrease proportionally with increase/decrease of voltage. The V-I characteristics of the devices is linear is called linear devices. The example of the linear device is a resistor. The linear devices follow the Ohm’s Law. If the voltage applied across resistor is sinusoidal the current flowing through it is also sinusoidal.

In a nonlinear devices, the current flowing through the device does not follow the Ohm’s law. The current flowing through the non linear devices is not follow the voltage waveform. If the applied voltage is sinusoidal, the current flowing through the non linear device is non-sinusoidal.

At the time of charging of the transformer the magnetizing current drawn by the transformer does not follow the sinusoidal voltage and current is non sinusoidal.

According to Fourier series, the non sinusoidal current can be resolved into the fundamental current and the integral multiples of the fundamental frequency. The integral multiples frequency of the fundamental frequency is called Harmonics.

What is fundamental frequency?

Fundamental frequency of the sinusoidal waveform is the first harmonic order frequency and it is equal to the supply frequency. The fundamental frequency is the lowest frequency f on which complex waveform is built. In india and UK the fundamental frequency is 50 Hz and in USA the fundamental frequency of alternating voltage is 60 Hz.

A sinusoidal waveform is an alternating voltage or current which varies according to sin function.

i = I_m sinwt
v = V_m Sinwt
w = 2Π f

Where,
v and i is instantaneous value of the waveform
V_m, I_m is the maximum value of the waveform
f is the lowest frequency or fundamental frequency

What is Harmonics?

Ideally voltage and current waveform is sinusoidal. However, because of the increased popularity of electronics power devices and other non-linear loads, the waveform quite often become distorted. The distorted waveform can be resolved into fundamental and integral multiples of fundamental frequency according to Fourier series. Thus, the distorted waveform will contain harmonics.

What is Harmonic Frequency?

If fundamental frequency is f , the harmonic frequency will be 2f, 3f, 4f, 5f, 6f and so on. If the frequency of the fundamental waveform is 50 Hz, the frequency of the harmonic waveform will be (2f= 2 x 50=100Hz), 3f= 3 x 50=150Hz, 200 Hz, 250Hz, 300Hz, 350 Hz etc.

Harmonic order can be assigned according to frequency of voltage or current waveform.

Harmonic order	Frequency(Hz)
2	100
3	150
4	200
5	250
6	300
7	350
8	400
9	450

2,4,6,8 order of harmonics are called even harmonics and the 3,5,7,9 are called the odd harmonics. 3,6,9 order harmonics are called triplen harmonics.

If current or voltage waveform is symmetrical about x-axis the even number of harmonics would be zero.

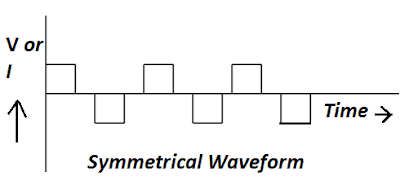
symmetrical waveform does not contain even harmonics

The converter and inverter waveform is symmetrical about x-axis, that is why it contains only odd order harmonics.

The instantaneous value of the harmonic frequency can be given as;

For a second order harmonics

Instantaneous value of 2nd order harmonics

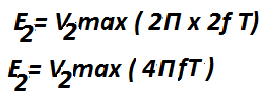
For a Third order harmonics

instantaneous value of 3rd order harmonics

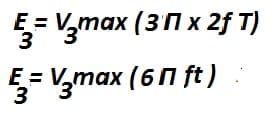
For a fourth order harmonics

Instantaneous value of 4th order harmonics

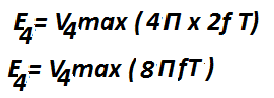
The instantaneous value of the complex waveform can be expressed as follows.

E T= Ef (fundamental) + Eh (harmonics)

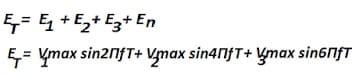
Instantaneous value of fundamental & all harmonics

Further, the harmonics order can be represented as positive and negative sequence harmonics. The harmonic frequency which has same phase sequence that of fundamental frequency has are called positive sequence harmonics. The harmonic frequency which has opposite phase sequence that of fundamental frequency has are called negative sequence harmonics.