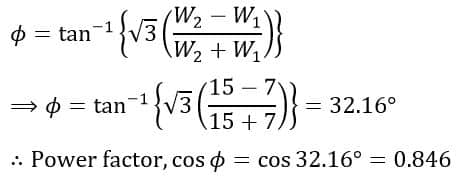In this article, will discuss the measurement of three-phase power using two wattmeter method (with balance load condition).
As we know, according to Blondel’s Theorem, the electrical power in a poly-phase electric circuit can be measured using N-1 wattmeters. Therefore, in a three-phase circuit, the power can be measured using only two (3-1) wattmeters. When the two-wattmeters are used for the measurement of three-phase power, the method is referred to as two wattmeter method.
Wattmeter – A wattmeter is an electrical measuring instrument used to measure electrical power consumed in an electric circuit. A typical wattmeter consists of two coils namely a current coil and a pressure coil (also called a potential coil). Wattmeters come in different power ratings ranging from watts to Mega-Watts.
Balanced Load Condition – In a three-phase circuit, when the impedances of all the circuit’s three phases are equal, this is called the balanced load condition.
The two-wattmeter method of three-phase power measurement is the most widely used method in electrical systems due to its several advantages. Now, let us discuss the two-wattmeter method with balanced load conditions in detail.
Two Wattmeter Method
In the two-wattmeter method of three-phase power measurement, the current coils of the two-wattmeters are connected in series of any two line conductors, and the potential coil of each is connected to the third line conductor. The connection diagram of two wattmeter method is shown in Figure 1.
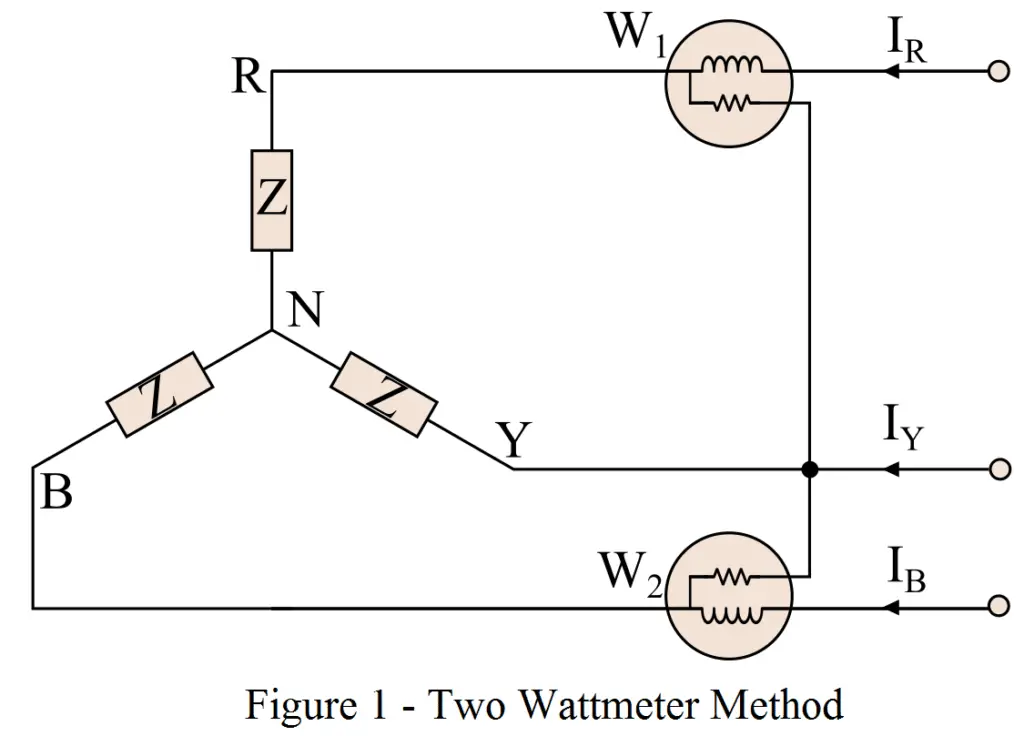
The total power consumed in the three-phase circuit will be the algebraic sum of the readings of the two wattmeters.
Derivation of Two-Wattmeter Method
Consider a balanced three-phase load (either connected in star or delta). If the power reading of the first wattmeter is W1 and the second wattmeter is W2. The power factor angle of the load impedance is ϕ.
Let, VRN, VYN, and VBN are the RMS values of the three load phase voltages, and IR, IY, and IB are the RMS values of phase currents. Let us assume the inductive phase, so the phase currents will lag behind their respective phase voltage by the phase angle ϕ. The phasor diagram of the two-wattmeter method with a balanced load is shown in Figure 2.
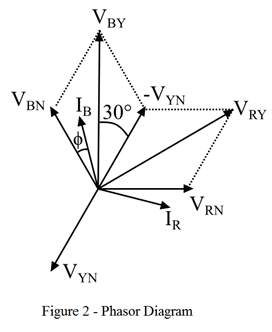
Referring to the circuit diagram, the current flowing through the current coil of the first wattmeter is IR.
The voltage across the potential coil of the wattmeter W1 is,
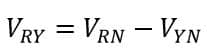
From the phasor diagram, it is clear that the phase angle between VRY and IR is equal to (30° + ϕ). Therefore, the power measured by the wattmeter W1 is given by,
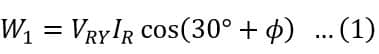
Similarly, the current flowing through the current coil of the second wattmeter W2 is IB and the voltage across the potential coil of the wattmeter W2 is,
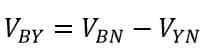
Again, from the phasor diagram, the phase angle between the voltage VBY and IB is equal to (30° – ϕ). Thus, the power measured by the wattmeter W2 is given by,
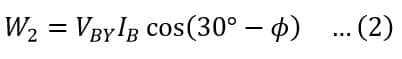
Since, the load is balanced, therefore,
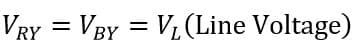
And
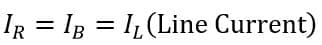
Therefore, equations (1) & (2) can be written as,
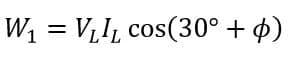
And
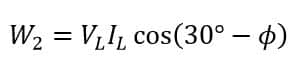
Therefore, the total power consumed in the circuit is given by the algebraic sum of two wattmeter readings, i.e.
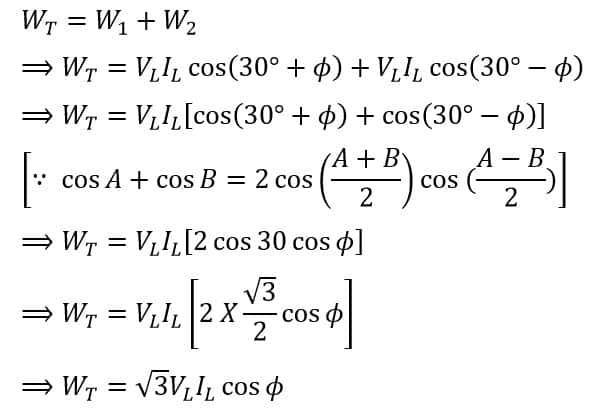
Thus, the total power in the three-phase circuit with a balanced load is,
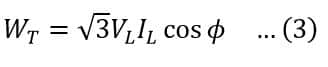
Measurement of Power Factor using Two Wattmeter Method
We can also determine the power factor angle of the load as follows:
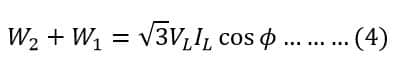
And,
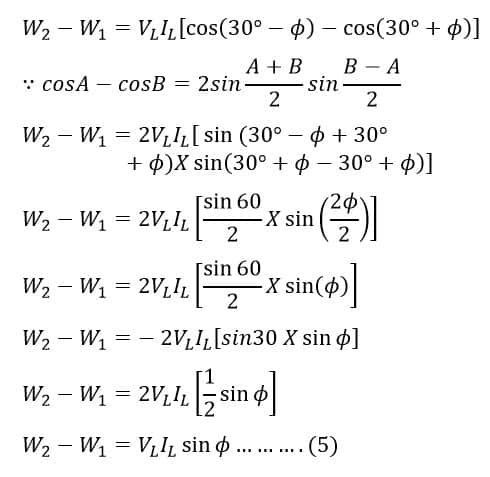
Therefore, by dividing equation (5) by 4, we get;
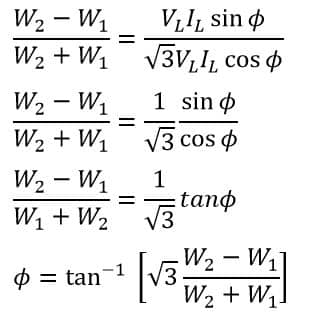
The power factor cos Φ is,
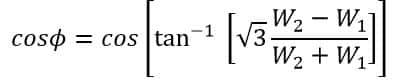
Advantages of Two Wattmeter Method
The major advantages of the two-wattmeter method of power measurement in an electric circuit are:
- The total power, i.e. the algebraic sum of readings of two wattmeters is independent of load impedance.
- The total power, i.e. the algebraic sum of readings of two wattmeters is independent of source imbalance.
- The total power, i.e. the algebraic sum of readings of two wattmeters is independent of the difference in two wattmeters.
- The total power, i.e. the algebraic sum of readings of two wattmeters is independent of the phase sequence of the three-phase system.
- The total power, i.e. the algebraic sum of readings of two wattmeters is independent of the source waveform.
Important Point – It should always be taken care of that if a neutral wire is available in the system, it should not carry any current while measurement is performed. If it carries current, then the neutral of the load must be disconnected from the neutral of the source.
Numerical Example
Two wattmeter method is used to measure power absorbed by a three-phase induction motor. The wattmeter readings are 15 kW and 7 kW. Find the total power absorbed by the motor, and the power factor of the motor.
Given data,

Thus, the total power absorbed by the motor is,
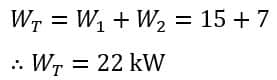
The power factor of the motor is,