Factors like the number of turns, area, length of the inductor, and permeability of the medium affect the inductor’s inductance. The inductance of the inductor basically depends on the amount of flux linking in the inductor’s turns per unit current. Now, we will discuss the factors on which the inductance of the inductor depends.
The following factors affect the inductance of an inductor.
- Number of Turns(N)
- Length of a coil (L)
- Area of the coil (A)
- Permeability of medium(µ)
Number of Turns(N)
The more turns (N) in the inductor have more inductance, the less turns has less inductance. Thus, we can say that the inductance of the inductor depends on the number of turns. The relationship between inductance and the number of turns can be expressed by following mathematical expressions.
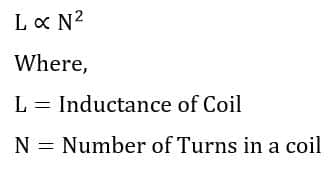
More turns will produce a more magnetic field. If one turn produces a magnetic field of 5 Tesla when 1-ampere current flows through the turn, then the magnetic field is 5 AT(ampere/turn). Now if we take 100 turns and feed 1 ampere current, then the magnetic field produced by the inductor is 100 AT. Thus, it is clear that the magnetic field produced by the inductor depends on the number of turns for a given amount of current.
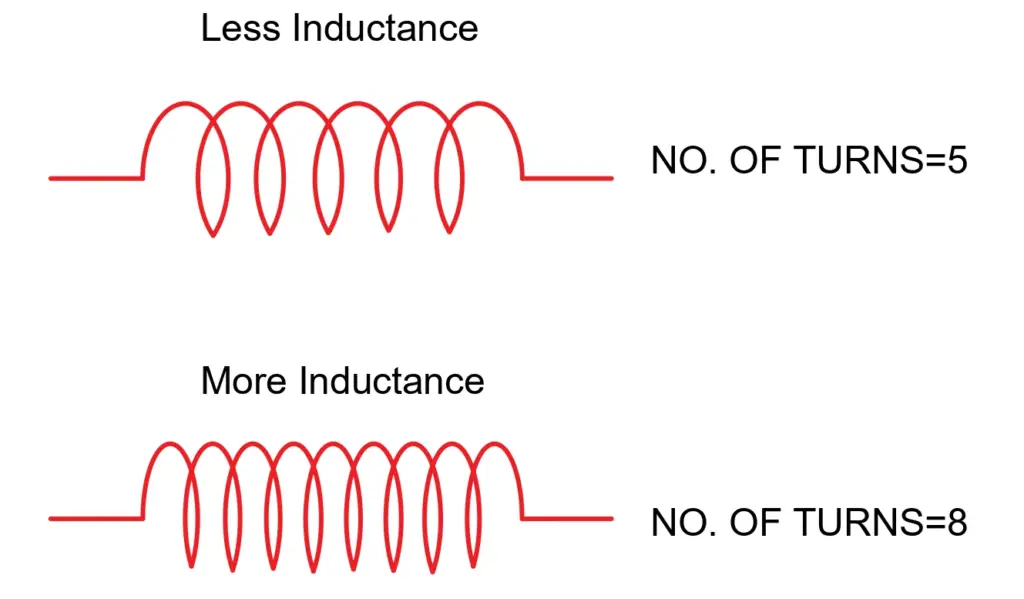
The inductance of the coil is directly proportional to the square of the number of the coil’s turns.
Coil Length
If we keep all other factors unchanged, the longer coil length causes less inductance, and a shorter coil length causes more inductance. The relationship between inductance and length of a coil can be expressed by following mathematical expressions.
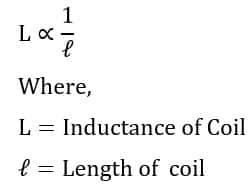
The longer coil length causes more opposition to the current because of more induced emf in the coil , and as a result, the magnetic flux linking in the coil is less. Thus, the less flux linkage in the coil leads to less inductance.
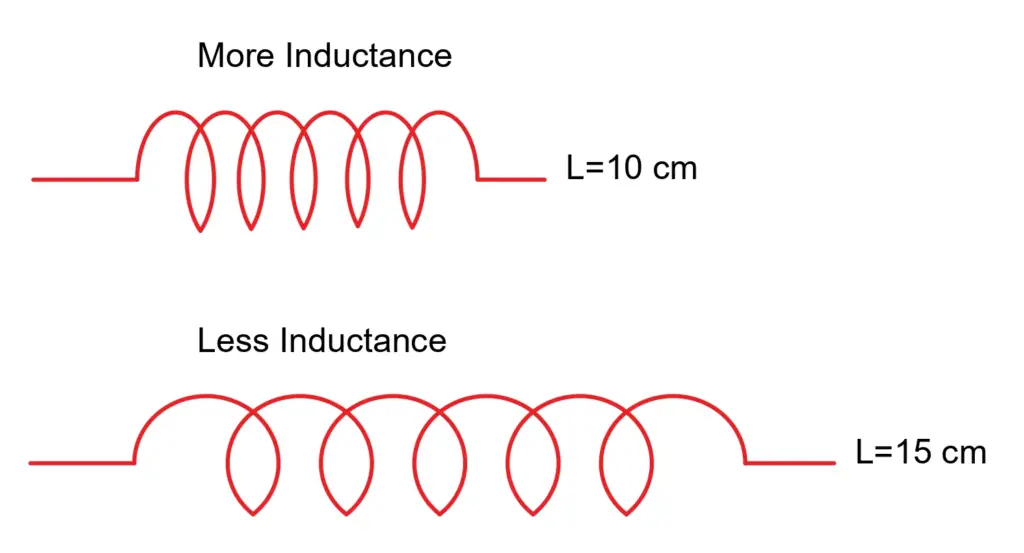
The inductance of the coil is inversely proportional to its length.
Coil Area
The more the cross-sectional area of an inductor, the more the inductance, keeping all other factors the same. The coil of a less cross-section area has less inductance as compared to the coil of a more cross-section area. The relationship between inductance and the area of a coil can be expressed by following mathematical expressions.

The coil with a greater cross-section area has less opposition to the flux linking to it. And, thus if the area of the coil is more, its inductance is more.
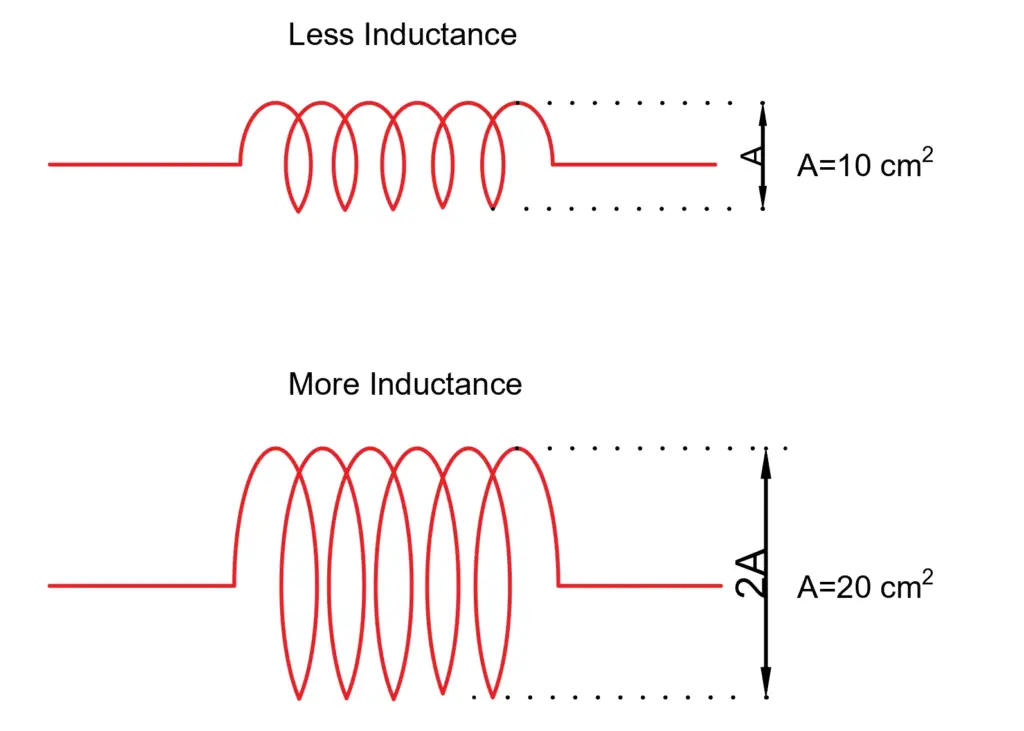
The inductance of the coil is directly proportional to the coil area.
Core Material
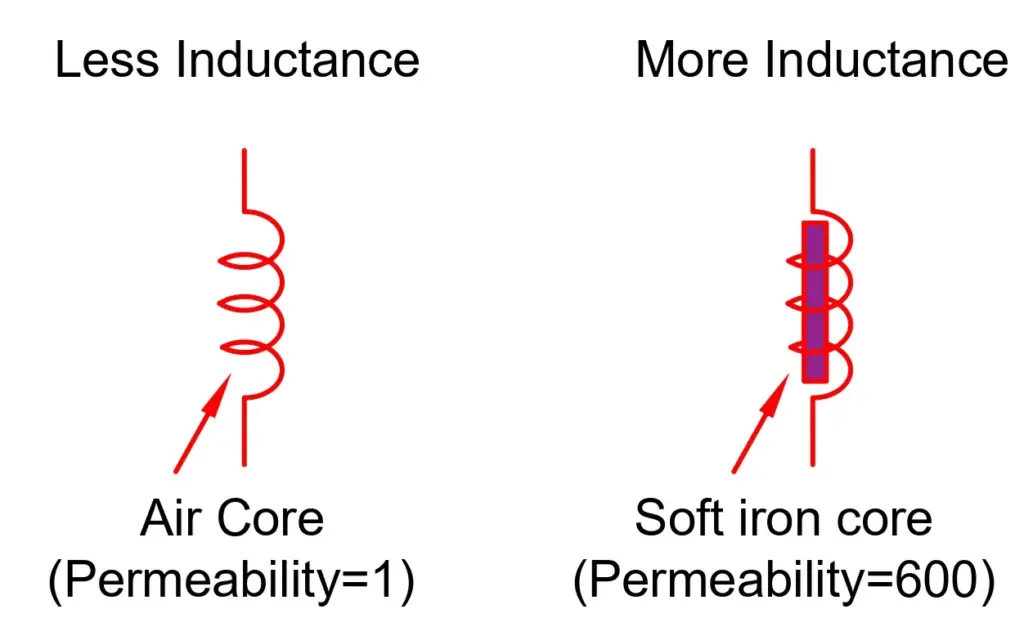
The inductance of a coil can be increased by increasing the permeability of the medium. The iron core inductor has more inductance than an air core inductor. It is because the permeability of the iron core inductor is more than the permeability of the air core inductor.
The permeability of the core material affects the flux linking in the coil. Therefore, the greater the permeability, the more the inductance.
Approximate Formula of Inductance of a Coil
A coil has a number of turns in a certain length and area. The dimensions of the coil are shown in depicted in the below picture.
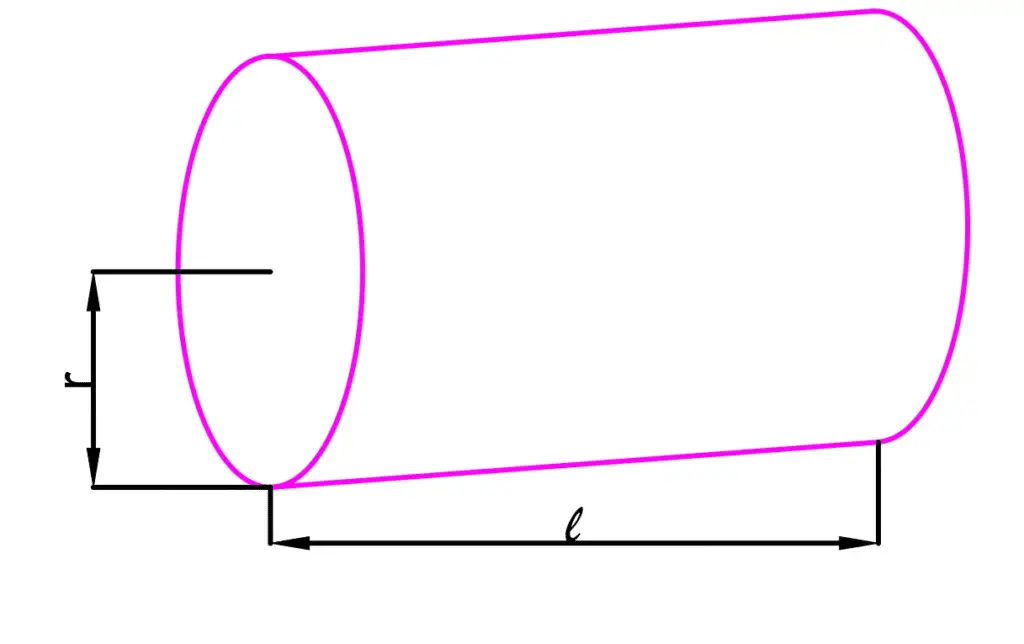
The inductance of a coil can be found with the following formula.

The permeability (µ0 µr) of the magnetic materials with change in the field intensity because the magnetic material has a nonlinear B-H curve. Thus the value of the permeability changes and can not be a constant value. Therefore, the inductance of a coil does not have a constant value despite having the same number of turns and the coil’s dimensions (length and area).
The hysteresis in the B-H curve can cause a significant effect on the value of inductance. Therefore, the design of the magnetic core for a coil is very important and it must be ensured that the flux density in the core must be much below the saturation point. in other words, the core must function in a linear region of the B-H curve or Hysteresis loop.
The variable inductor is made by making a provision for change in the number of turns of a coil, or by use of a sliding core that moves in and out of a coil. The below picture shows the variable inductor that has a mechanism of the number of turns changing.

The sliding copper contacts connect the different points along the coil’s length. Making contact at different points changes the length and number of turns of a coil and thus, the inductance changes accordingly.
We can increase the inductance by moving the magnetic core to the middle of the inductor winding. And, for reducing the inductance of a coil, the magnetic core is moved out of the inductor winding.
