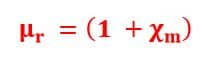In this article, we will derive the mathematical expression to establish the relation between relative permeability and magnetic susceptibility of the material.
Magnetic permeability (µ) is the material’s magnetization capability. The higher permeability materials quickly get magnetized. On the other hand, the lower permeability material, such as air or vacuum does not magnetize easily. The higher permeability materials have more number of magnetic dipoles and magnetize quickly.
Magnetic susceptibility (χ) is another important term that tells how much magnetization of the material takes place with an applied magnetizing field. Some materials have a tendency to magnetize quickly, whereas some materials do not magnetize at all or get less magnetized. The susceptibility of the material shows the degree of the magnetization of the material with the applied magnetic field(H).
Formula Derivation for Relation between Magnetic Permeability and Susceptibility
Let us take a piece of material. Now, we keep the material in the magnetic field. The material receives the magnetic field that magnetizes the material. The process of formation of the magnetic field inside the material is called the magnetization process. The magnetic field inside the material is always more than the applied magnetizing intensity. The reason behind this fact is that dipoles of the material also have magnetizing power.
Thus, the total magnetic field inside the material is the sum of the applied magnetic field and magnetic field due to the magnetization of the material. In other words, we can say the net field is a resultant of magnetization due to the applied field (B0) and magnetization due to induced magnetism (Bi).
The applied magnetizing field to the material is;
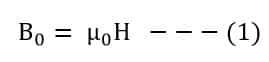
Magnetization (Bi) in the material due to applied field (B0)

The total magnetic field inside the material is the sum of Bi and B0
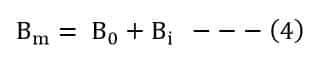
Putting the value of equations(2) & (3) in equation(4),
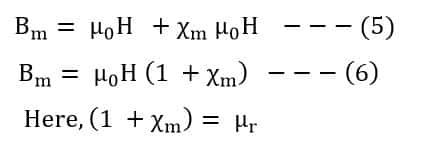
Thus, the relationship between relative permeability & magnetic susceptibility is given below.