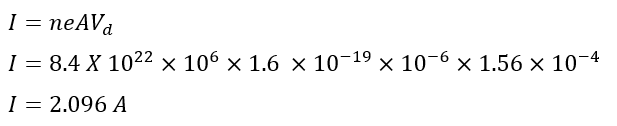When an electric field is applied to a conductor, free electrons begin to move slowly in the opposite direction of the field. The average velocity with which these electrons drift is known as drift velocity, and this motion forms the basis of the relation between current and drift velocity.
This drift of electrons results in the flow of electric current. Understanding this relationship helps explain how microscopic electron motion leads to measurable current in a conductor.
In this article, we will explore the derivation, formula, and diagram related to the relationship between current and drift velocity, along with solved numerical examples for better clarity.
What is Drift Velocity?
The flow of electric current is proportional to the drift velocity and other factors. Drift refers to the slow movement of particles.
When an external electric field is applied around a conductor, electrons move slowly toward the positive potential. The average velocity of these electrons is known as the drift velocity, and they move in the axial direction of the plane.
The drift velocity is the average velocity of electrons moving through a conductor in response to an electric field.
Read detailed artcile on: Drift Velocity: Definition, Formula, Derivation
Relation Between Current and Drift Velocity Diagram
Understanding the relationship between current and drift velocity becomes much clearer with a visual representation.
The diagram below illustrates how the motion of electrons under an applied electric field contributes to the flow of electric current in a conductor.
In the diagram:
- A straight conductor is shown with a defined length (L) and cross-sectional area (A).
- The electric field (E) is applied from the left to right, indicated by the arrow pointing →.
- Electrons, represented as small dots, move in the opposite direction (←) to the electric field due to their negative charge.
- Their average velocity in this direction is called drift velocity (Vd).
- As these electrons drift, they collectively constitute the electric current (I) flowing through the conductor.
This visual helps to correlate how microscopic electron motion (drift velocity) contributes to macroscopic current, reinforcing the derived formula:
Drift Velocity and Current Relation Formula
The relation between drift velocity and electric current is given by the formula:
Where:
- I= Electric current (in amperes, A)
- n = Number of charge carriers per unit volume (in m3)
- A = Cross-sectional area of the conductor (in m2)
- vd= Drift velocity of charge carriers (in m/s)
- e = Charge of each carrier (Coulombs, C)
Rearranged for Drift Velocity
This equation shows that drift velocity is directly proportional to current and inversely proportional to the number of charge carriers, area, and charge.
Now we will derive the mathematical relation between current and drift velocity, using basic physical parameters of a conductor.
Relation between Current and Drift Velocity Derivation
Let’s take a conductor whose length is L and the cross-section area is A. The volume of the conductor is;
Step 1: Volume of the Conductor
Step 2: Total Free Charge
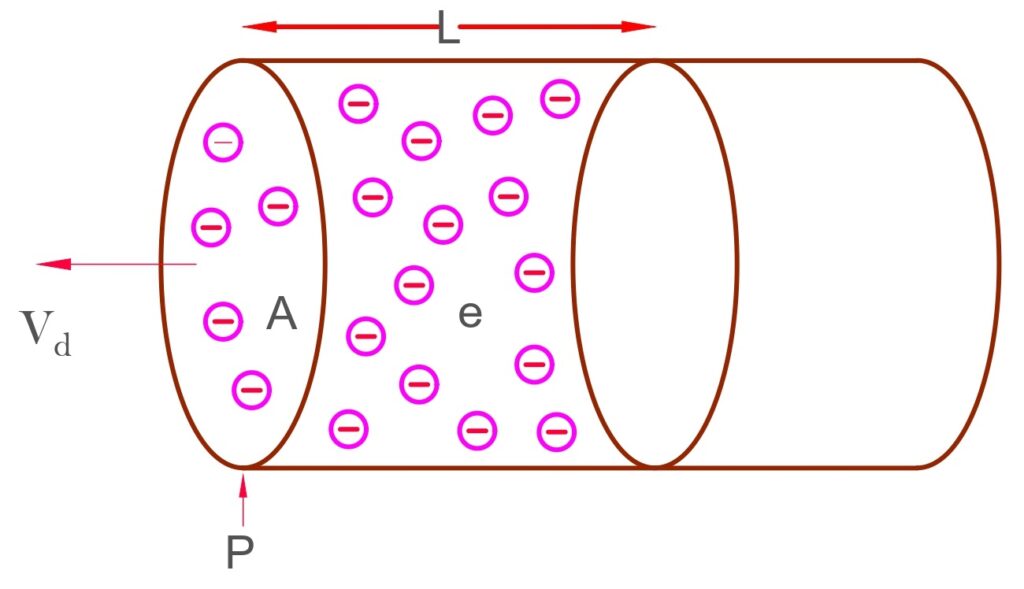
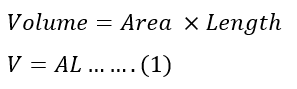
Let the number of electrons be n in unit volume, then the total electrons in the conductor is;
Total number of free electrons in the conductor,
The charge of an electron is ‘e’; therefore, the total free charge in a conductor is,
Step 3: Time and Current Relation
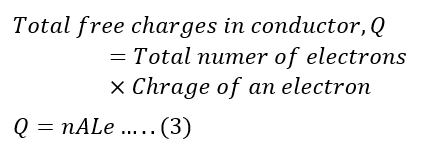
The time taken by an electron to cross the conductor is;
Current flowing in the conductor is.
Step 4: Final Drift Velocity Formula
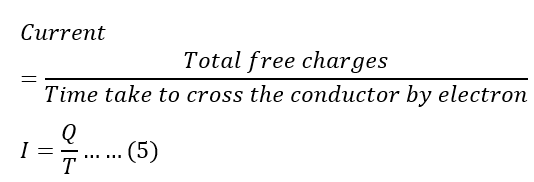
Putting the values of Q and T from equations 3 and 4 in equation 5, we can establish the relation between current and drift velocity.
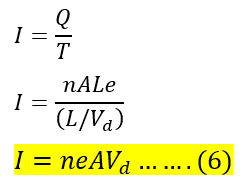
Drift Velocity is,
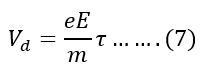
Putting the value of Vd from equation 7 in equation 6, we get;
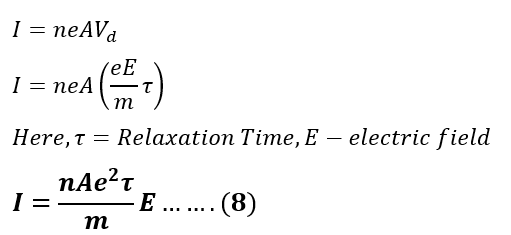
The equations, 7 and 8, show the relation between current and drift velocity.
Solved Examples Based on Relation between Current and Drift Velocity
Problem 1: A conductor wire has 1032 free electrons/m3, and its cross-section area is 2 mm2. Calculate the drift velocity of electrons if the current 20 A flows through it. (e = 1.6 x 10-19 C)
Given data-
n=1032
A= 2 x 10-6 m2
I= 20 A
e= 1.6 x 10-19 C
Solution:
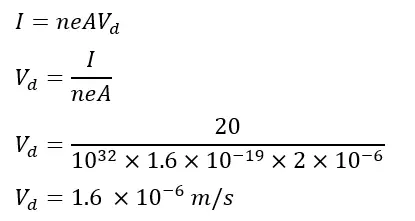
Problem 2: There are 8.4×1022 free electrons per cm3 in a conductor. If the drift velocity of electrons in a wire of 1mm2 size is 1.56 X 10-4 meters/second, then calculate the current flowing in the wire. (e=1.6 x 10-19 C).
Given data-
n=8.4 x 1022 X 106 per m3
A =10-6 m2
Vd=1.56 x 10-4 m/s
e= 1.6 x 10-19 C
Solution:
Conclusion
The relation between current and drift velocity reveals how microscopic electron drift leads to observable electric current. As derived, the current is directly proportional to the drift velocity, electron charge, number density, and conductor area.
This drift velocity and current relation is vital in understanding conduction in metals and semiconductors. With formula, derivation, diagram, and solved examples, we’ve covered everything needed to grasp the current and drift velocity relation in depth.
FAQs
The formula is I = n × A × e × Vd.
Drift velocity is directly proportional to electric current; as drift velocity increases, current increases, provided other factors are constant.
Yes, drift velocity can be negative depending on the direction of electron flow.
Related Articles: