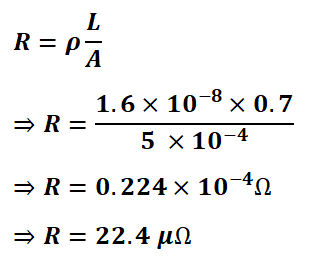This article describes the relationship between resistance and length of a material with the resistance wire formula.
Resistance is the property of the material that opposes the flow of electrons through it. The greater the opposition, the higher the resistance. The resistance of a wire or a conductor depends on the material’s resistivity, length, and cross-section area. The length of the conductor is a physical dimension that extends between two points of the conductor.
The three factors that determine the resistance of a conductor are resistivity, length, and cross-section. The resistivity( ρ) of the material depends on the type of material. The conductive materials have different resistivity. The electrical resistivity of copper is 1.68 X 10-8 (ohm-m), and aluminum resistivity is 2.63 X 10-8.
If we take the two wires that have the same resistivity and cross-section area but different lengths. What will the resistance value of each wire be? Will it be equal for both wires or different? Let’s dive deep into the concept of resistance to know the facts.
The flow of electrons occurs through a wire or conductor. If electrons travel for more lengths, they will experience more opposition because they collide at numerous points throughout the length. Thus, it is obvious that the longer wire or conductor will have more resistance. The greater length of the conductor causes more resistance.
We can determine the relationship between resistance and length using the resistivity and resistance formula of the wire.
Table of contents
Resistance Formula of Wire
The relationship between resistance and length of a wire can be expressed mathematically as follows:
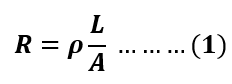
Where
- R is the resistance in ohms.
- L is the length of the material in meter
- A is the cross-sectional area measured in m2
- 𝜌 is the resistivity of the material in ohm-metre
From equation 1, it is clear that the resistance of a wire or conductor is directly proportional to its length. The resistance value of the material will change with a change in the length. If we increase the length, the resistance will increase; if we decrease the length, the resistance will decrease.
Resistance And Length Relation
From equation 1, we can mathematically state the relationship between resistance and length by the following expression.
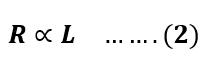
From equation 2, we can say that-
- The value of the resistance will increase with an increase in length.
- The value of resistance will decrease with a decrease in length.
If a wire with a length of 30 centimeters has a resistance of 0.2 ohms, then a wire with a length of 60 centimeters and the same material and cross-sectional area will have a resistance of 0.4 ohms.
Resistance And Length Formula
The resistance and length formula can be obtained by rearranging the resistivity and cross-section of the conductor.
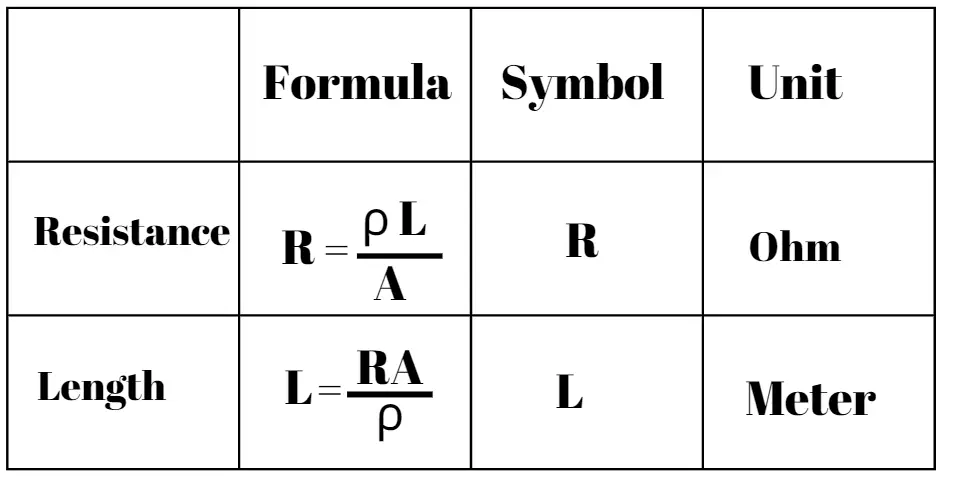
Solved Problems
Q.1: A 3-meter-long wire has a cross-sectional area of 1.7×10-3m2 and resistivity of 1.86×10-7Ohm-metre. Calculate the wire resistance.
Given data,
Length of the wire L = 3 m
Cross-sectional area A = 1.7×10-3m2
Resistivity 𝜌 = 1.69×10-8Ohm/meter.
Substituting the values in the resistance and length formula of the wire
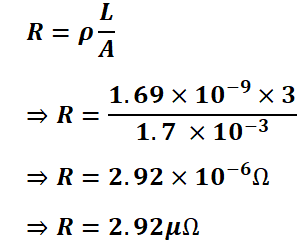
Thus, the resistance of the wire is 2.92 microohm.
Q.2: Calculate the resistance of a silver wire of length 0.7 meters and cross-section area 5 x 10-4 m2. The resistivity of silver is 1.6 X 10-8 Ohm/meter.
Given data,
Length of the wire L = 0.7 m
Cross-sectional area A = 5×10-4m2
Resistivity 𝜌 = 1.6×10-8 Ohm/meter
Substituting the values in the resistance and length formula of the wire