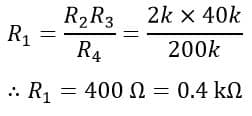In this article, we will discuss Maxwell’s Bridge, its circuit construction, types, equations, phasor diagram, advantages, disadvantages, and applications.
Maxwell’s bridge is a type of AC bridge that is used for the measurement of the self-inductance of a circuit. Maxwell’s bridge is basically an advanced version of the Wheatstone bridge.
The operation of Maxwell’s bridge is based on the principle of comparison, which means the unknown inductance’s value is determined by comparing it with a standard value of inductance or capacitance.
Types of Maxwell’s Bridge
Depending on the method used to determine the value of unknown inductance, there are the following two types of Maxwell’s bridges-
- Maxwell’s Inductance Bridge
- Maxwell’s Inductance Capacitance Bridge
Now, let us discuss each type of Maxwell’s bridge in detail.
What is Maxwell’s Inductance Bridge?
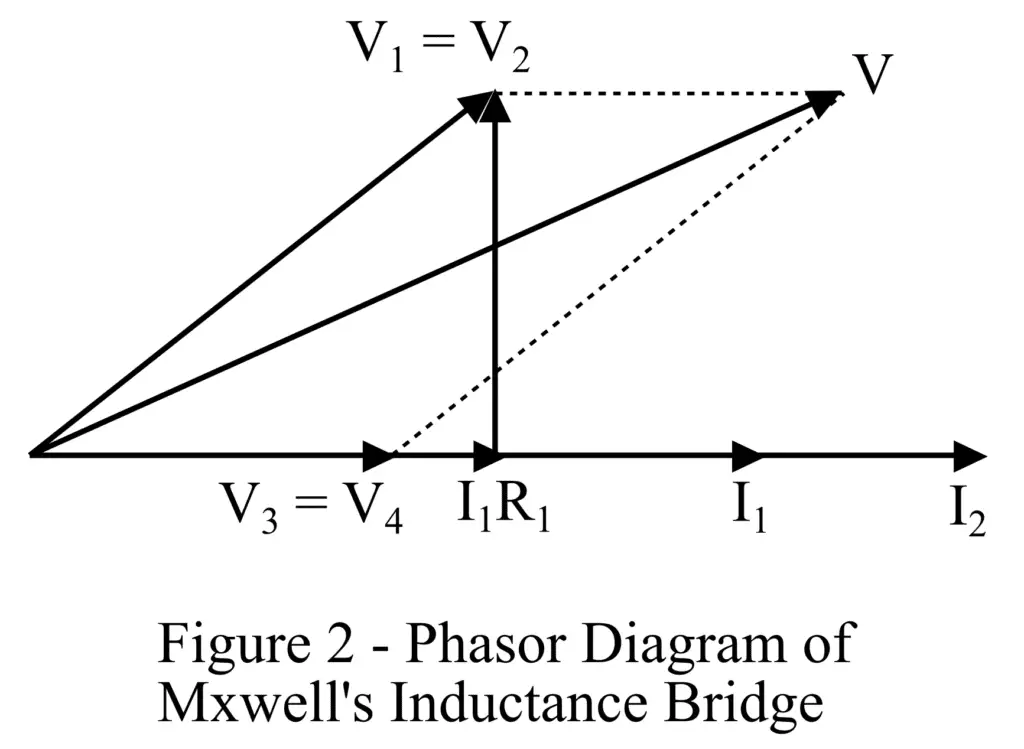
In Maxwell’s inductance bridge, the value of the unknown inductance and resistance of an inductor is determined by comparing it with a known inductance. The circuit construction of Maxwell’s inductance bridge is shown in Figure 1.
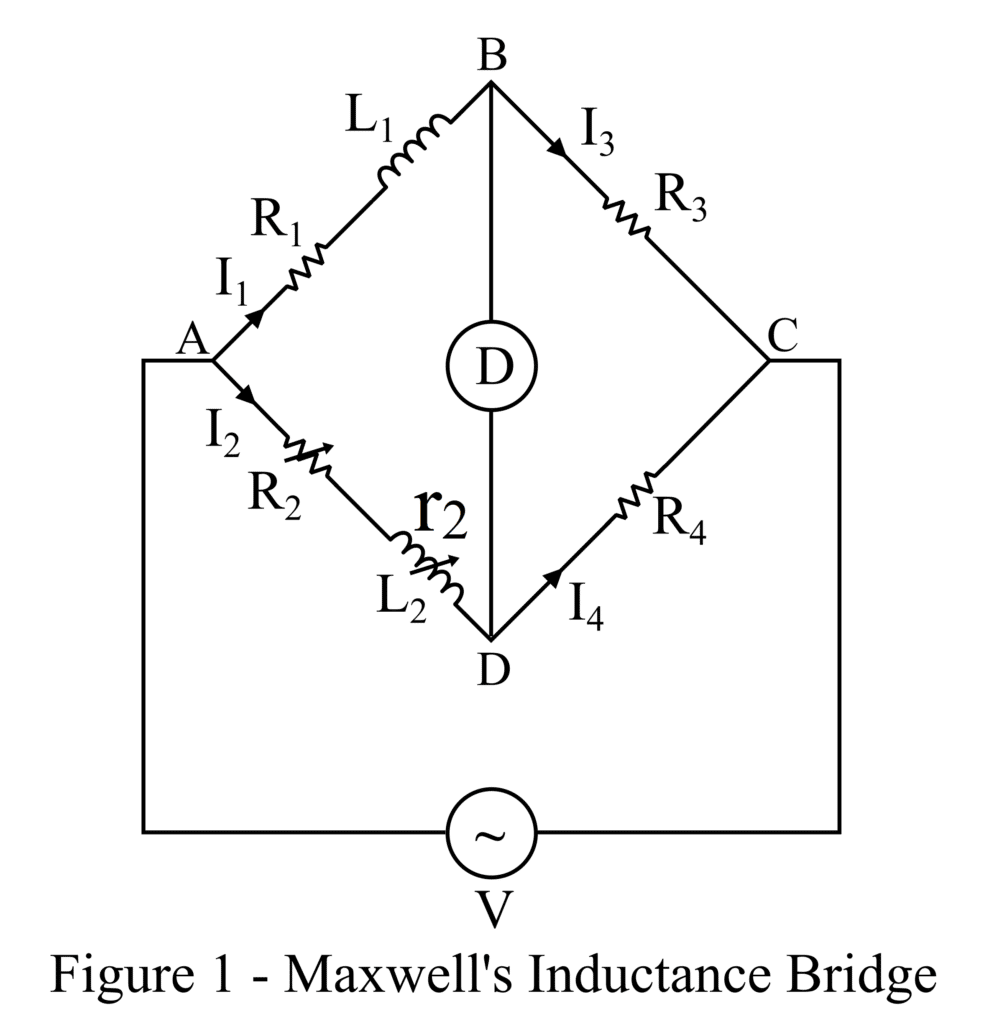
In the circuit diagram of Maxwell’s inductance bridge, L1 is the unknown inductance, R1 is the internal resistance of the unknown inductance, L2 is the inductance of a variable inductor of resistance r2, R2 is a standard variable resistance, R3 and R4 are the standard non-inductive resistances.
We may derive the equations to determine the values of unknown self-inductance and resistance from the circuit diagram of Maxwell’s inductance bridge as follows-
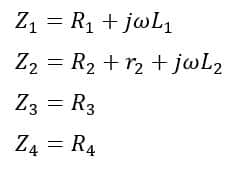
Under the balanced condition of the bridge, we have,
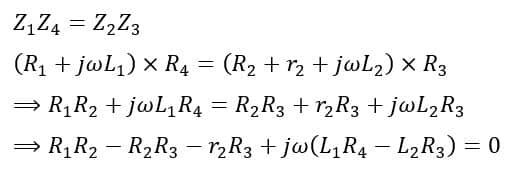
On equating the real and imaginary parts of the above equation, we get,
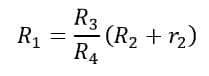
And,
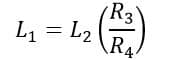
The phasor diagram of Maxwell’s inductance bridge is shown in Figure 2.
What is Maxwell’s Inductance Capacitance Bridge?
Maxwell’s inductance capacitance bridge is another type of Maxwell’s bridge in which the unknown self-inductance and resistance of an inductor are determined by comparing them with a standard known capacitor. The circuit construction of Maxwell’s inductance capacitance bridge is shown in Figure 3.
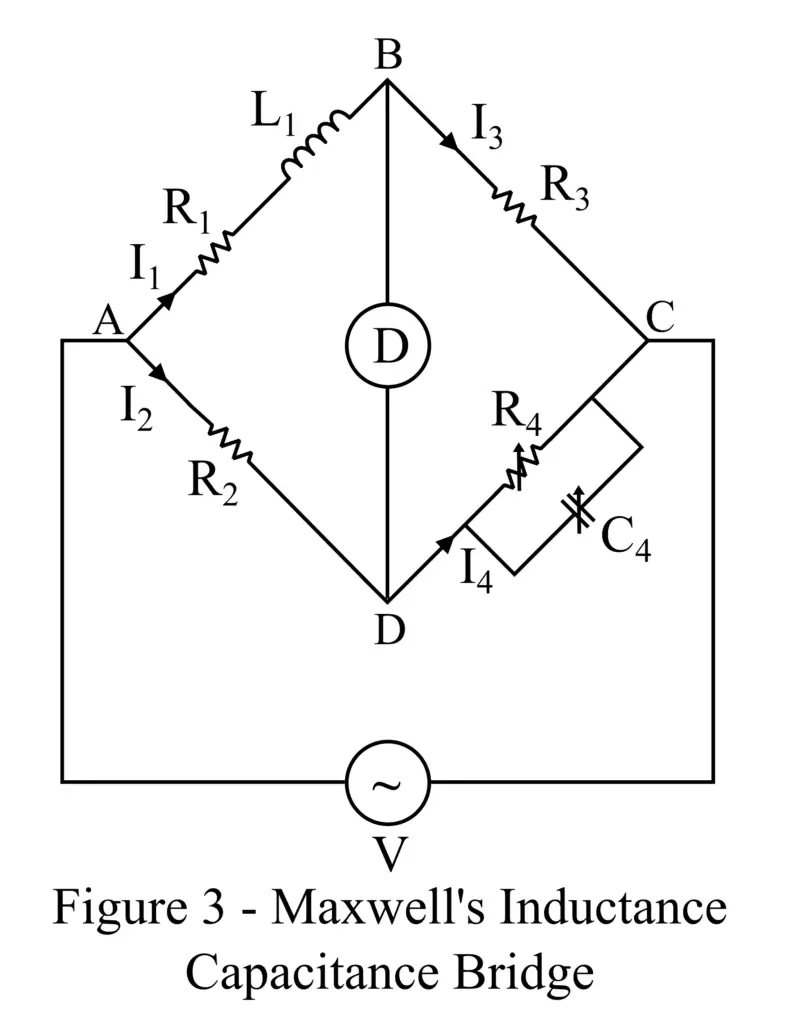
In the circuit diagram of Maxwell’s inductance capacitance bridge, L1 is the unknown inductance, R1 is the resistance of the unknown inductance, R2 and R3 are the standard non-inductive resistors, R4 is a non-inductive variable resistor, and C4 is a standard variable capacitor.
From the circuit diagram of Maxwell’s inductance capacitance bridge, we may derive the equations to determine the values of unknown inductance and resistance as follows-
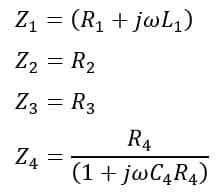
Under the balance condition of the bridge, we have,
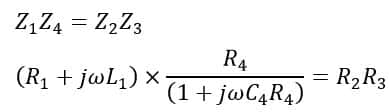
On rearranging the equation, we get,
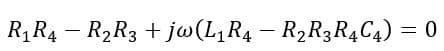
On equating the real and imaginary parts of the equation, we have,
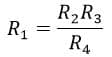
And,
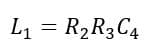
Using these two equations, we may determine the values of unknown inductance L1 and resistance R1.
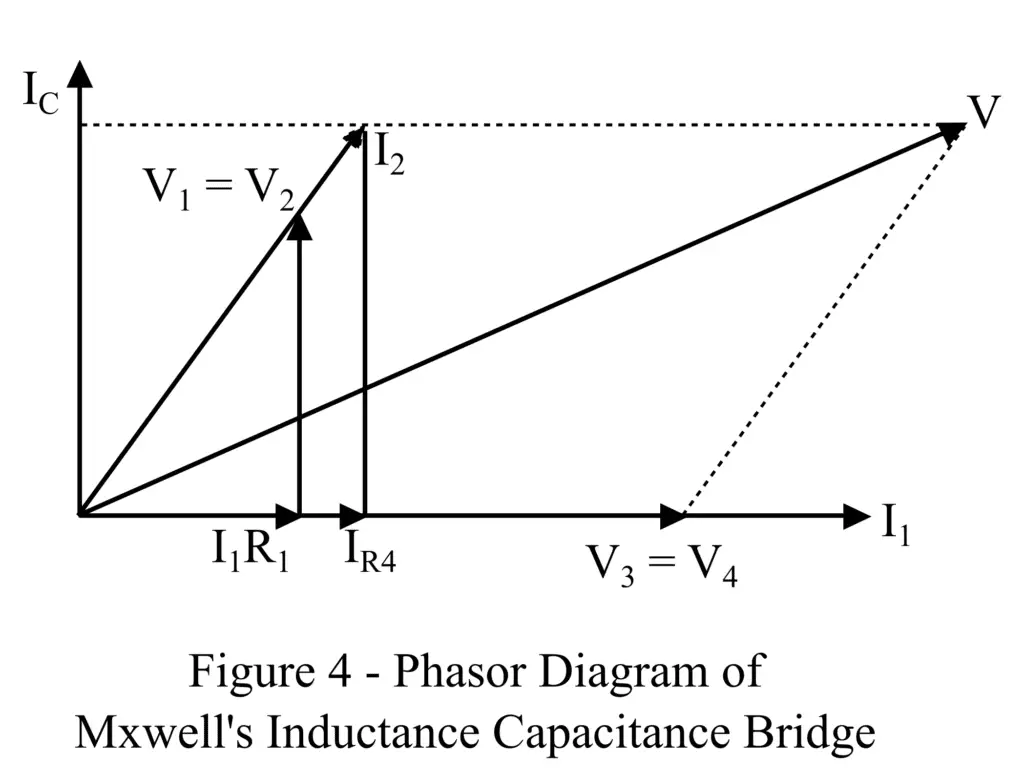
The phasor diagram of Maxwell’s inductance capacitance bridge is shown in Figure 4.
Advantages of Maxwell’s Bridge
The following are the important advantages of Maxwell’s inductance bridge-
- The balance equation of Maxwell’s bridge is independent of the frequency.
- The equation of self-inductance and resistance are independent of each other.
- Maxwell’s inductance capacitance bridge can be used to determine a broader range of inductances.
- Using a variable capacitor makes the bridge balance condition, free from disturbances due to stray magnetic fields.
Disadvantages of Maxwell’s Bridge
The following are some major disadvantages of Maxwell’s bridge-
- We can use Maxwell’s bridges to measure the inductance of medium-quality inductors/coils.
- In Maxwell’s inductance capacitance bridge, the use of a variable capacitor makes the bridge costlier.
Applications of Maxwell’s Bridges
The following are some important applications of Maxwell’s Bridge-
- Maxwell’s bridges are extensively used for the measurement of self-inductance.
- Maxwell’s bridge can be used to measure self-inductance at audio as well as power frequencies.
Numerical Example on Maxwell’s Bridge
A Maxwell’s inductance capacitance bridge is used to measure an inductive impedance. The bridge constants at the balance condition are:
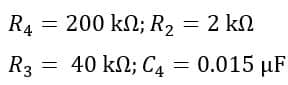
Find the self-inductance and resistance of the unknown inductor.
Solution –
Self-Inductance of the inductor is,
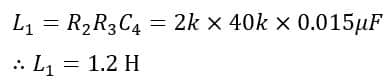
And the resistance of the given inductor is,