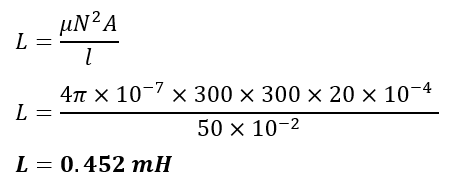The inductance formula calculates the inductance of the inductor. This article describes the inductance formula and how to calculate inductance.
When electric current flows through the inductor, a magnetic field is produced around it. The strength of the magnetic field depends on the inductance, current, and number of turns in a coil. The letter L denotes the inductance value, and its unit is Henery. One Henry equals one volt from a current change of one ampere per second.
When an alternating current passes through a coil, it induces a varying flux that, in turn, generates an electromotive force (EMF) within the coil. The rate of change of current and inductance of a coil determines the magnitude of the induced EMF.
Formula for Inductance
The formula for inductance is;
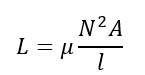
Where
L = inductance in Henry (H)
μ = permeability (Wb/A.m)
N = number of turns in the coil
A = area encircled by the coil
l = length of the coil(m)
Inductive reactance measures the opposition to the flow of alternating current caused by an inductor. The formula for inductive reactance is,
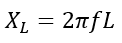
Where,
Reactance is X in ohm (Ω)
the frequency is f in Hz,
Inductance is L in Henry (H)
The voltage induced in a coil depends on the inductance and rate of current change. The formula for induced voltage is as follows;
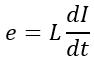
Where,
V = voltage(volts)
L = inductance value (H)
I = the current is (A)
t = time taken (s)
When the current I flows through a coil that has N turns and produces flux Φ, then the inductance of the coil is,
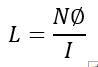
The equivalent inductance of the series connected inductors is;
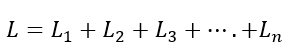
Where, L1, L2, L3….. Ln are the inductance values.
The equivalent inductance of the parallel connected inductors is;
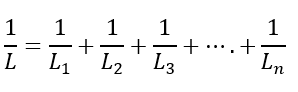
Where, L1, L2, L3….. Ln are the inductance values.
Inductance Formula Derivation
The magnetic field is produced around an inductor or a coil when current flows through it.
The magnitude of the flux depends on the magnetomotive force and the reluctance of the magnetic path through the flux flows.
When current flows through the coil, it creates a magnetomotive force(MMF), which depends on the magnitude of the current and the number of turns in a coil.
The magnetomotive force (MMF) is;
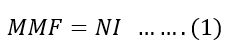
The magnetomotive flux creates flux, which flows through the magnetic circuit and completes its path in a closed circuit. The reluctance of the magnetic path resists the flux; therefore, the flux depends on the MMF and reluctance.
The reluctance of the magnetic circuit is;
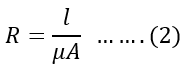
Where
μ = permeability (Wb/A.m)
A = area encircled by the coil
l = length of the coil(m)
The flux in the magnetic circuit is the ratio of MMF and reluctance. Therefore,
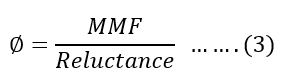
Putting the value of MMF and reluctance in equation (3), we get,
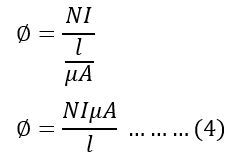
According to Faraady’s law of electromagnetic induction, the voltage is induced in a coil when there is a change in the current. The change in the current change in the flux produced. Therefore, the induced voltage depends on the number of turns and the rate of change of flux.
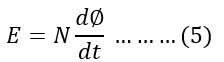
The induced voltage also depends on the inductance and the rate of change in current.
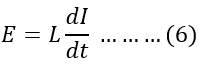
Comparing equation(5) and (6),
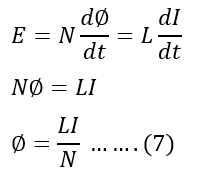
Putting the value of flux from equation(4) in equation(7), we get,
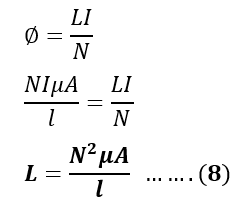
Inductance – Solved Examples
Example 1: Calculate the equivalent inductance if inductors of 3H, 1H, and 4H are connected in series.
Given Data-
L1 = 3H, L2 = 1H, L3 = 4H
The inductance of the series connected inductors is,
L = L1 + L2 + L3
= 3H + 1H + 4H
L = 8 H
Example 2: Calculate the equivalent inductance if inductors of 3H, 1H, and 4H are connected in parallel.
Given Data-
L1 = 3H, L2 = 1H, L3 = 4H
The inductance of the parallel connected inductors is,
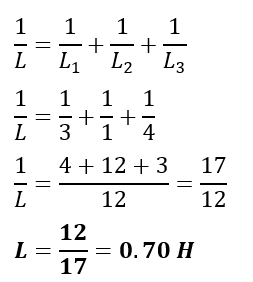
Example 3: An inductor has reactance 12560 Ω at 50 Hz. Calculate its inductance.
Given Data-
XL = 12560 Ω, f = 50 Hz
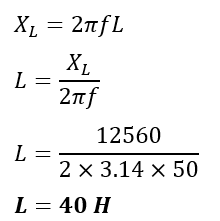
Example 4: The current changes in a coil from 3 amperes to 1 ampere in 0.2 seconds induce 5 volts. Calculate its inductance.
Given Data-
I1 = 3 A, I2 = 1 A,
t1 = 0, t2 = 0.2 s
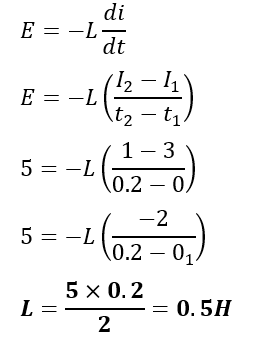
Example 5: When a 500-turn inductor coil carries 8 amperes of current, it generates 300 mWb of magnetic flux. Calculate the inductance of the inductor.
Given Data-
N = 500,I = 8 A,Φ=300 mWb
Applying the inductance formula,
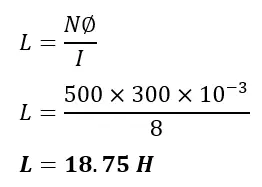
Example 6: What is the inductance of a solenoid with 300 turns, a cross-sectional area of 20cm², and a length of 50 cm?
Given Data-
N = 300, l = 50 cm, A=20cm²
Inductance formula