The dimensional formula of inductance is [ML2T−2A−2]. In this article, we will derive this dimensional formula of inductance.
What is a Dimensional Formula?
The dimensional formula is a way of expressing the physical quantity in terms of its fundamental dimensions. In physics, there are seven fundamental dimensions- Mass (M), Length (L), Time (T), Electric Current (A), Temperature(T), Amount of Substance (N), and Luminous Intensity (J).
Dimensional analysis is a powerful tool in physics and engineering for checking the consistency of equations and deriving relationships between physical quantities. If two physical quantities are added or equated, their dimensional formulas must be the same to be dimensionally consistent.
The formula or equation of that physical quantity must be known to derive the dimensional formula of quantity.
Formula or Equation of Inductance
Inductance is a property of an inductor or a coil that opposes changes in current passing through it. Inductance is denoted by the symbol “L” and is measured in units called henrys (H).
When the current flowing through an inductor changes, it induces an electromotive force (EMF) in the inductor. This induced EMF generates a magnetic field around the inductor. The inductance of a coil is a measure of the magnetic field produced in response to a change in current.
The mathematical relationship between inductance (L), induced EMF (e), and the rate of change of current (di/dt) is given by Faraday’s law of electromagnetic induction, labeled as equation (1):
Where:
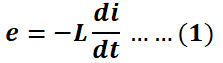
- e is the induced electromotive force (EMF) in volts,
- L is the inductance in henrys,
- di/dt is the rate of change of current with respect to time.
Therefore, from equation (1), the formula for inductance is:
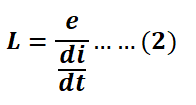
Dimensional Formula for Inductance
The formula of inductance has two terms- EMF and rate of change of current. We will find the dimensional formula of these terms to get the dimension of inductance.
Dimensional formula of EMF(e):
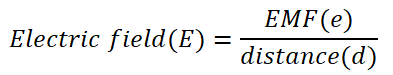
so,
Putting the fundamental value in the above expression:
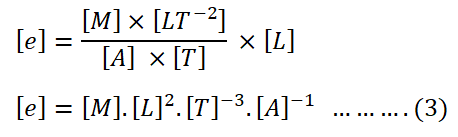
Dimensional formula of Rate of change of current (di/dt)
The dimensional formula of current (i) is given by:
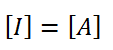
The dimensional formula of time (t) is given by:
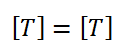
The dimensional formula of the rate of change of current:
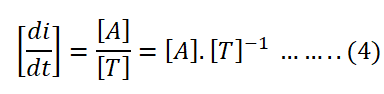
Dimensional formula of inductance:
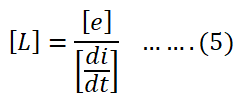
Putting the value of [e] and [di/dt] from equation(3) &(4) in equation(5):
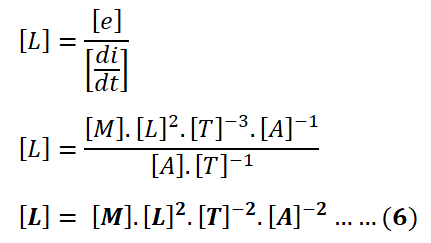
The dimensional formula of inductance is:
![Dimensional Formula of Inductance: [ML²T⁻²A⁻²]](https://www.electricalvolt.com/wp-content/uploads/2023/11/image-202.png)
Physical Significance of Inductance Dimensions
The inductance dimensional formula [ML2T-2A-2] reveals the fundamental physics of how an inductor behaves in an electrical circuit:
- Energy Storage (ML2T-2): The term ML2T-2 is the exact dimensional formula for Work or Energy (Joules). This confirms that inductance is fundamentally a measure of a coil’s capacity to store energy within its magnetic field.
- Current Dependency (A-2): The negative exponent on the Current dimension (A) indicates that inductance represents energy per unit current squared (L = 2E/I2), perfectly aligning with the formula for the total energy stored in the magnetic field (E = 1/2 LI2).
Understanding these dimensions allows engineers to verify complex electrical equations and analyze transient behaviors in power systems.
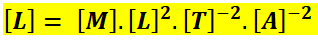
Summary
The dimensional formula for inductance, including self-inductance and mutual inductance, is the same. Since these quantities are measured in Henry, the dimensional formula of Henry is identical to that of inductance. The inductance dimensions (self-inductance and mutual inductance) and Henry is [ML²T⁻²A⁻²]
![dimensional formula of inductance is [ML2T−2A−2].](https://www.electricalvolt.com/wp-content/uploads/2023/11/Dimnsional-Formula-of-Inductance-1024x536.png)
Frequently Asked Questions (FAQs)
The SI unit of inductance is the Henry (H), named after the American scientist Joseph Henry. One henry is defined as the inductance of a coil where a current change of one ampere per second induces an electromotive force of one volt.
he dimensional formula of Henry is exactly identical to inductance: [ML2T-2A-2]. Because Henry is the unit used to measure both self-inductance and mutual inductance, they all share the exact same fundamental dimensions.
Yes, both self-inductance and mutual inductance share the exact same dimensional formula: [ML2T-2A-2]. While they describe different physical setups, both represent the ratio of induced voltage to the rate of change of electrical current.
Read Next: