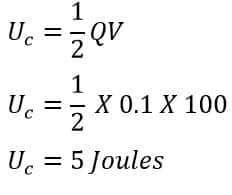In this article, we will derive the energy stored in a capacitor formula. The type of energy stored in a capacitor is electrostatic potential energy. The electrostatic potential energy depends on the charge stored and the voltage between the capacitor plates. Thus a capacitor stores electrical energy in the form of electrostatic energy between its plates.
When we disconnect the capacitor after fully charging it, it does not discharge quickly but takes some time to discharge, In fact, the capacitor discharges through its internal resistance. The internal resistance of the capacitor has a very high value.
Energy Stored in a Capacitor
Let us understand how the energy stored in a capacitor is related to electric charge Q and the potential difference between plates V. To understand this, we consider a capacitor that has air as a dielectric medium between the plates. Let the space between its plates has a volume Ad. This volume has a uniform electrostatic field E & the total energy Uc is contained inside this space.
The energy density in this space can be calculated by dividing the total energy by volume. Mathematically,

Therefore, the energy stored in a capacitor is’
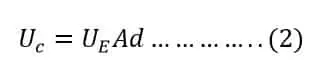
The energy density UE in a region of free space occupied by an electrical field E depends only on the magnitude of the field.
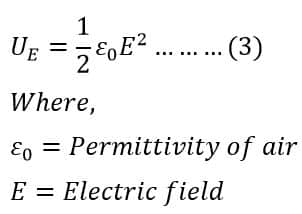
The electric field between the plates of a capacitor is;
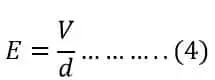
Putting the value of electric field E in equation 3, we get;
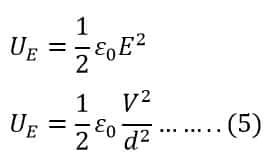
By placing the value of UE in equation 2, the total energy stored in a capacitor is;
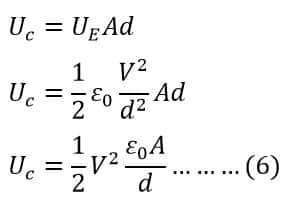
We know, the value of capacitance is;
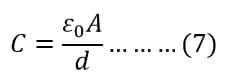
Putting the value of capacitance C from equation 7 in equation 6, we get;
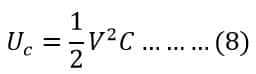
We know,
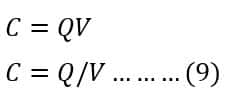
Therefore, the total energy stored in a capacitor is ;
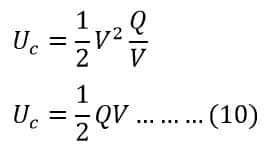
Therefore, the formula of energy stored in a capacitor can be expressed by following the mathematical formula,
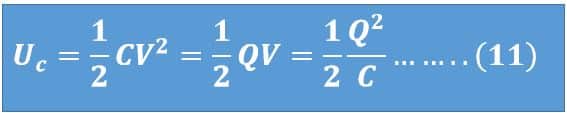
Alternate Method for Derivation of formula for Energy Stored in a Capacitor
We need to do work when we move an infinitesimal charge dq from lower potential to higher potential. Therefore, on moving the charge from the negative plate to the positive plate amount of work dW must be done on dq. The work done for moving the charge is;
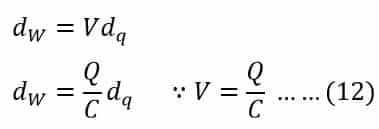
This work is the energy stored in the electrical field of the capacitor. The total work done to charge a capacitor to a charge Q is;
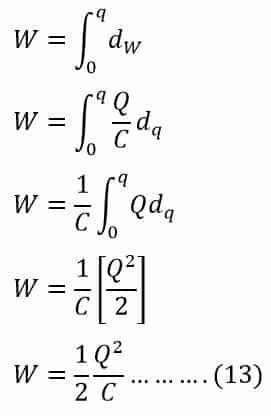
Putting the value of Q= CV in equation 13, we get;
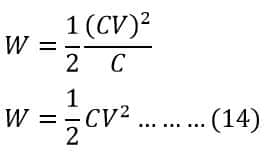
Conclusion
From the above discussion, it is clear that energy stored in a capacitor is due to the electrostatic field developed between the plates of a capacitor. The energy stored in a capacitor is because of potential difference, therefore it is also called potential energy.
The energy stored in a capacitor is proportional to the value of capacitance. Thus, the higher-value capacitance stores more energy for the same voltage.
The property of capacitors of storing energy makes them suitable for various electrical and electronic circuits such as chargers, capacitor banks, computer circuits, etc.
Solved Problems on Energy Stored in a Capacitor
Numerical Example(1)
A capacitor has a capacitance of 1.0 μF is connected across a battery of 60 volts. Calculate the energy stored in the capacitor.
Given Data-
C= 1.0 μF = 1 X 10-6 Farad
V= 60 Volts
Uc = ?
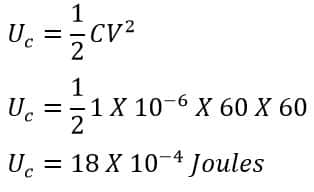
Numerical Example(2)
A capacitor stores a charge of 100 mC when it is connected to 100 volts supply source. Determine the energy stored in the capacitor.
Given Data-
Q= 100 mC = 100 X 10-3 C= 0.1 C
V= 100 Volts
Uc =?