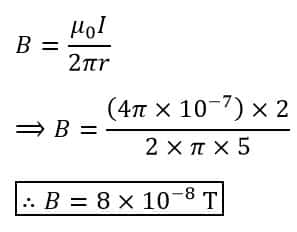In this article, we will discuss the magnetic field due to a steady current in an infinitely long straight wire.
By using the Biot Savart Law, we can determine the magnetic field or magnetic flux density (B) at a specific point due to a steady current in an infinitely long straight wire.
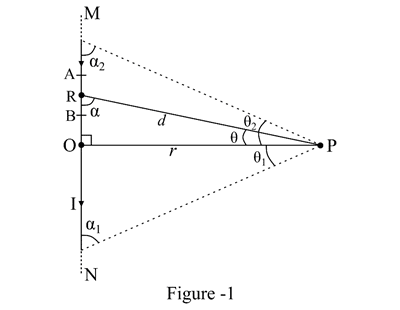
Consider a straight conductor MN of infinite length carrying an electric current of I amperes as shown in the figure-1. In this case, we need to determine the magnetic flux density (B) at a point P which is at a distance of r meters from the conductor wire.
Let a small current element AB of length Idl. If the distance between the point P and the mid-point of the current element is d, and the line segment RP makes an angle θ perpendicular to the direction of the current as shown in the figure. Then, according to the Biot Savart law, the magnetic field flux density (dB) at P due to the current element Idl is given by,
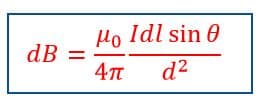
Now, we can determine the magnetic flux density at the point P due to the entire length of the conductor MN as follows:
In ΔROP
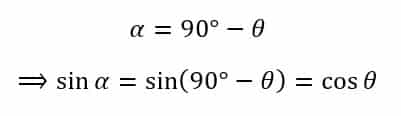
Also,
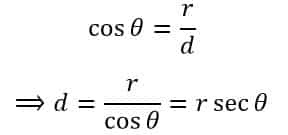
And,
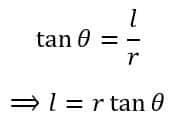
On differentiating on both sides, we get,

Therefore,
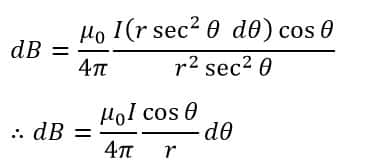
Thus, the magnetic field at point P due to the entire length of the conductor MN is given by,
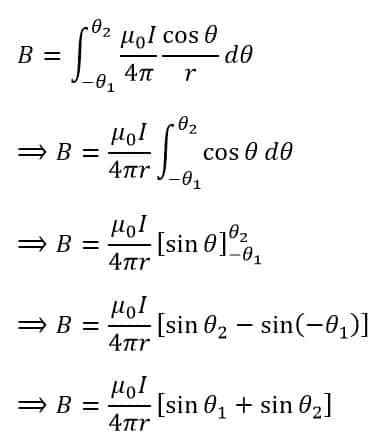
Now, there are the following cases possible for the conductor of infinite length,
Case 1 – If the given conductor is infinitely long, in that case,
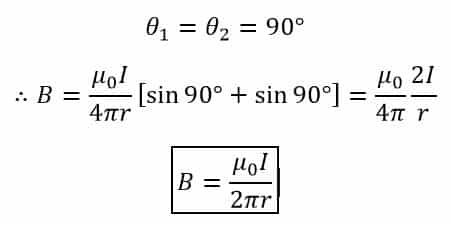
Case 2 – If the given conductor is of infinite length, but its one end is in front of the point P. In this case, the one end of the conductor starts from the point O. Hence,
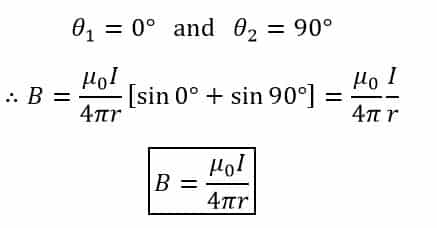
Numerical Example – An electric current of 2 A flowing through a conductor of infinite length. Calculate the magnetic field density due to the effect of the whole of the conductor at a point, where the distance between the conductor and the point is 5 m.
Solution – Given data,
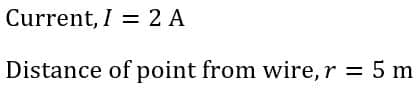
Therefore, the magnetic field density at the given point is given by