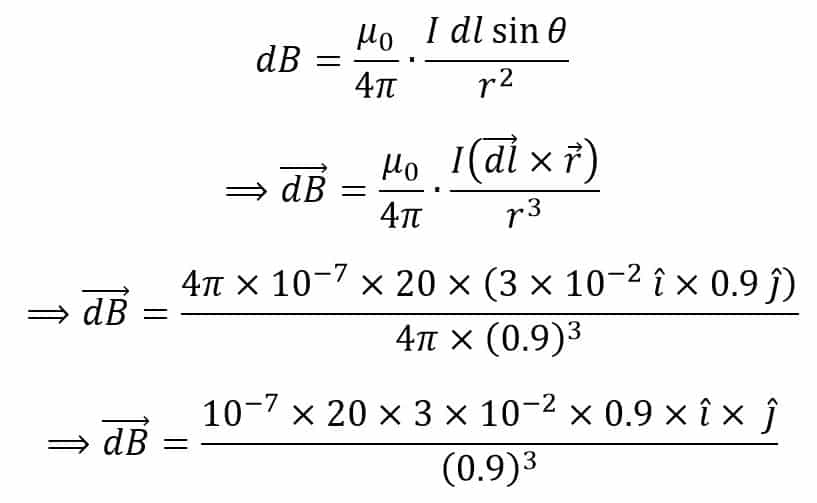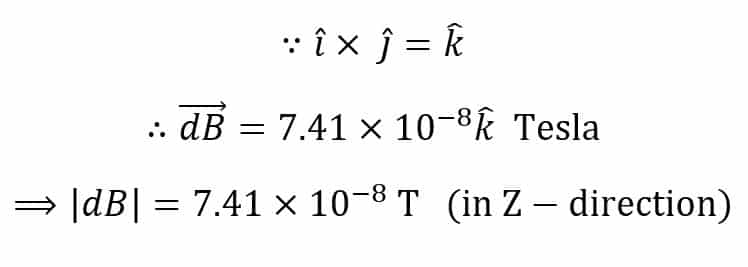The Biot Savart Law describes the magnetic field generated by a constant electric current. It is a well-known fact that when an electric current flows through a conductor, it generates a magnetic field around it. When a constant electric current flows through the conductor, the magnetic field produced by it can be described by the Biot Savart law.
Basically, the Biot Savart law gives the relationship between magnetic flux density and length of the conductor, magnitude, direction, and proximity of the electric current. The statement and mathematical derivation of the Biot Savart law were described by two French physicists “Jean Baptiste Biot” and “Felix Savart” in 1820.

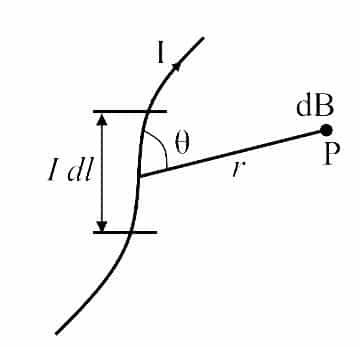
The mathematical expression of the Biot Savart law gives the value of magnetic flux density at a point due to a nearby current carrying conductor. Where, the magnetic flux density is directly proportional to the length of the conductor, electric current, and the sine of the angle between the direction of the electric current and the vector joining a given point of the magnetic field and the conductor and is inversely proportional to the square of the distance between the point of magnetic field and the current carrying conductor.
Statement of Biot Savart Law
The Biot Savart law states that the magnetic flux density produced by a tiny current element at any point is:
- Directly proportional to the length of the current element, the magnitude of the current and sine of the angle between the direction of current and the line joining the current element and the point of the magnetic field, and
- Inversely proportional to the square of the distance between the current element and the point of the magnetic field.
Where the direction of the magnetic field at that point is the same as the direction of the dl x r.
Derivation of Biot Savart Law
From the statement of the Biot Savart law, we have,
(i). dB is directly proportional to I, i.e.
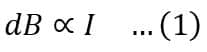
(ii). dB is directly proportional to dl, i.e.
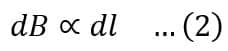
(iii). dB is directly proportional to Sinθ, i.e.
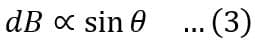
(iv). dB is inversely proportional to r2, i.e.
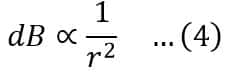
Hence, by adding equations (1), (2), (3), and (4), we get,
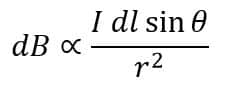
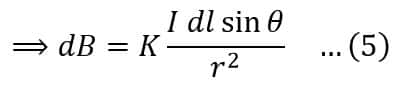
Where K is a constant of proportionality, its value depends on the magnetic properties of the medium and the system of units employed.
In the SI system of units, the value of K is given by,
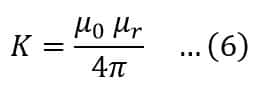
Hence, from Eqn. (5) & (6), we get,
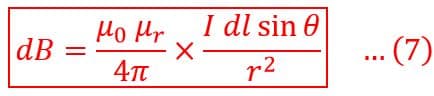
The expression in equation (7) is known as Biot Savart’s law.
Magnetic field at Point P Due to the Entire length of the Current Carrying Conductor
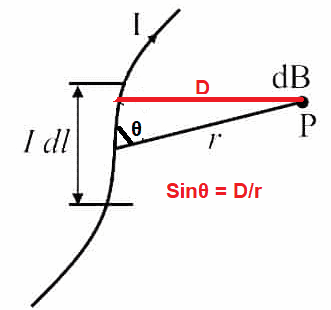
The flux density( B ) at the ‘P’ end due to the whole length of the current carrying wire can be written as,
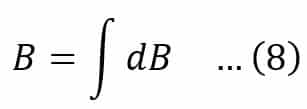
Putting the value of dB from equation (7) in equation(8), we get
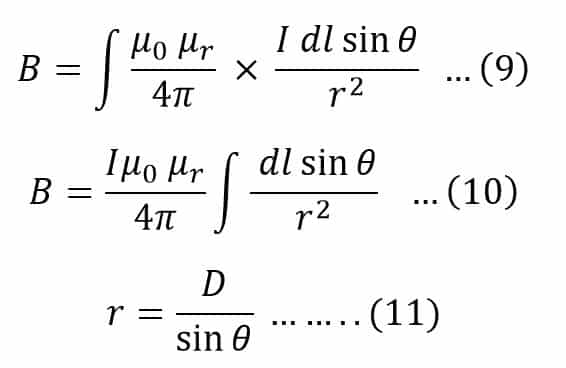
By putting the value of r in equation(10), we get
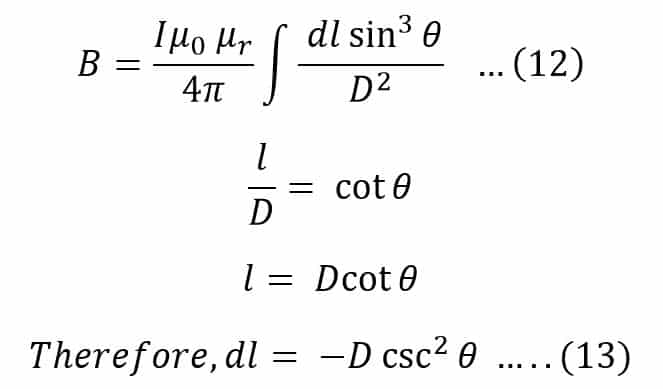
Putting the value of dl in the equation(12), we get,
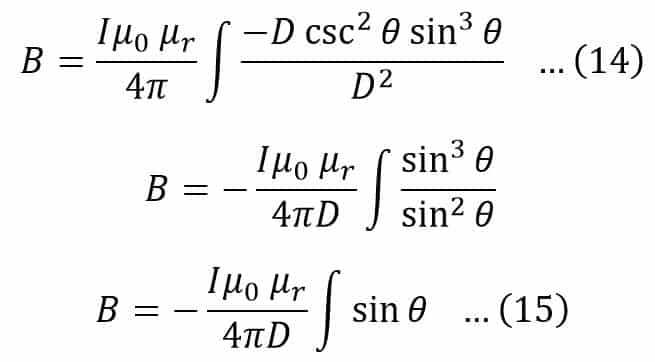
This value of angle θ depends upon the length of the wire and the position of the point P. Let angle θ varies from θ1 to θ2. Hence, the magnetic flux density at point P due to the whole length of the conductor is;
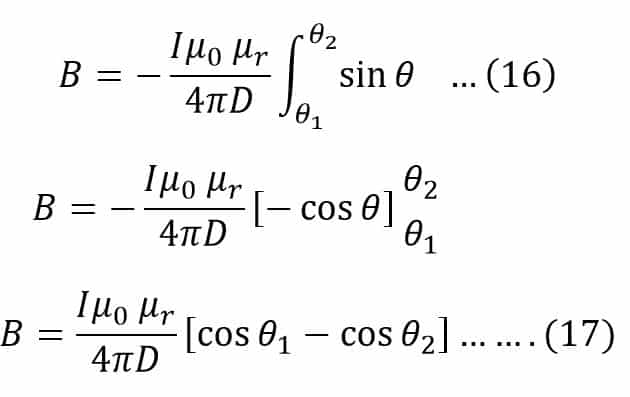
Let’s imagine the wire is infinitely long, The angle θ will vary from 0 to π for an infinite long wire. We get the following expression by putting the value of limits of the angle in expression no(17).
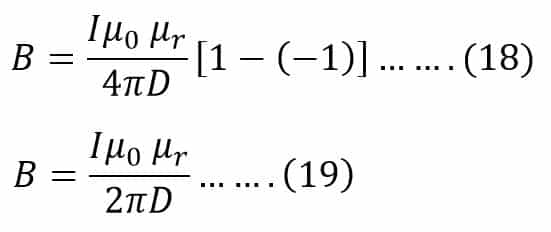
Importance of Biot Savart Law
Biot Savart’s Law is important due to the following reasons:
- It is the fundamental law of magnetostatics.
- This law can be equally applied to various small conductors that carry electric current.
- This law can be applied for symmetrical current distribution.
Applications of Biot Savart Law
Some common applications of Biot Savart law are as follows:
- The law can be used to calculate the magnetic field due to a constant current in an indefinitely long straight conductor.
- This law can also be used to determine the magnetic field along the axis of a circular current carrying coil.
- The law can be used to calculate magnetic effects even at atomic or molecular levels.
- This law can also be used in aerodynamics to calculate the velocity induced by the vortex lines.
Solved Problem on Biot Savart Law
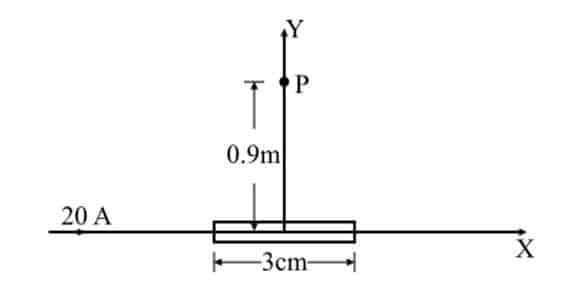
A current element whose length is 3 cm and has a current of 20 A is placed at the origin along the X-axis. What will be the magnetic flux density at a distance of 0.9 meters from the origin on the Y-axis?
The conditions described in the question are shown in the following figure,
Here,
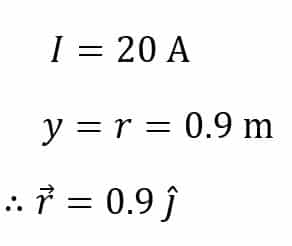
And,
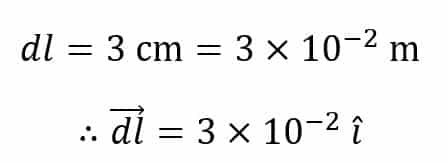
Now, according to Biot Savart’s Law, the magnetic field density at point “P” is