- kW (Active Power): kW measures the real power consumed by electrical equipment to perform actual work.
- kVA (Apparent Power): kVA represents the total power drawn from the supply, including both active and reactive components.
- Reactive Power (kVAr): kVAr is the power stored and returned by reactive elements like inductors and capacitors; it does not perform real work.
- Relationship Between kW, kVA, and kVAr: kW, kVA, and kVAr are related through the power triangle and power factor (kW = kVA × PF).
- Conversions and Calculations: Formulas allow easy conversion between kW and kVA using the power factor for single-phase and three-phase circuits.
- Quick Comparison Table: A simple table highlights the differences between kW and kVA at a glance, including definitions, symbols, consumption, relationships, and examples.
- Practical Applications: Understanding these concepts helps correctly size transformers, motors, and other electrical equipment, and improves power factor management.
Understanding the difference between kW and kVA is crucial in electrical engineering. kW (kilowatt) measures the real or active power that performs work in a system, while kVA (kilovolt-ampere) measures the apparent power drawn from the supply, which includes both active and reactive components.
A clear understanding of the relationship between kW, kVA, and kVAr (reactive power) is essential for correctly sizing transformers, motors, and other electrical equipment.
This article provides a detailed explanation of kW and kVA, including formulas, single-phase and three-phase examples, and practical calculation methods.
What is kW (Active Power)?
kW is the unit of active power that is consumed by the load for doing real work. The real power drawn from the system is also known as an active power or average power.
What is kVA (Apparent Power)?
kVA is the apparent power drawn from the supply source for the functioning of the electrical equipment. The electrical equipment draws reactive power to meet its magnetizing current requirement.

Understanding Reactive Power (kVAr)
To understand the concept of apparent power, let us first understaand the concept of reactive power. The equipment that functions on the magnetic principle always draws reactive power, known as kVAr.
The system stores the kVAr power instead of consuming it.
The reactive elements like inductors, capacitors,s and non-linear loads like a diode, bipolar junction transistors, MOSFETs, IGBTs, etc., draw reactive current from the supply source.
These electrical components consume reactive power(kVAr), but these do not consume real power except some minor active power. Thus, the inductor, capacitor, and nonlinear loads draw reactive power(kVAr) from the supply source.
Reactive Power kVAr in Inductor and Capacitor
An inductor, when connected to an AC supply, draws current, which lags the voltage by 90 degrees. The active power drawn by the inductor is zero; the inductor draws only reactive power (kVAr) except for very minor active power in the form of heat loss.
Contrary to an inductor, a capacitor, when connected to an AC supply, draws current, which leads the voltage by 90 degrees. The active power drawn by the capacitor is zero.
The capacitor draws only reactive power (kVAr) except very minor active power in the form of heat loss.
The reactive components inductor and capacitor do not draw any real or active power from the system. Still, these circuit components draw current from the system to meet their reactive power(kVAr) requirement.
Thus, the total current drawn from the supply source is the vector sum of the active and reactive current.
kW, kVA, kVAr in Power Triangle
The power triangle diagram effectively illustrates the relationship between active power (kW), reactive power (kVAr), and apparent power (kVA).
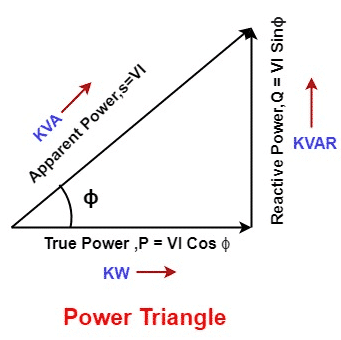
From the above power triangle, the relationship between kW, kVAr, and kVA is as follows:
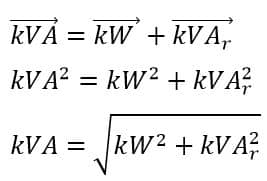
Where,
kVA – Apparent Power
kW – Active Power
kVAr – Reactive Power
The relationship between kW, kVAr, and kVA is as follows.
If the reactive current drawn is zero, the apparent power is equal to the real or active power. In the case of the resistive loads, the reactive current is zero, and the real power and the apparent power are equal.
In the case of the inductive and capacitive loads, the apparent power(kVA) is always more than the active power. The apparent power increases with an increase in the reactive power with the same active power. As reactive power increases, the power factor decreases
Relation between KVA and KW
The relation between KVA and KW for single-phase and three-phase AC circuits is given below.
Single Phase Circuit- kVA and kW
The relationship between apparent power and active power is:
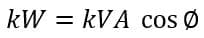
Where,
CosΦ is the power factor.
The power factor is unity for the resistive loads, and thus, the kVA is equal to the kW.
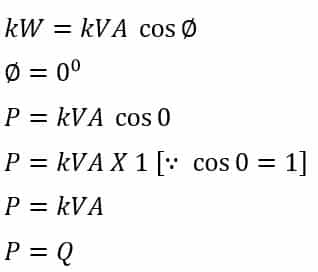
The inductor and capacitor current lags and leads the voltage by 90 degrees, respectively. For single phase circuit, the active power drawn by the inductor is;

Thus, the active power drawn by the pure inductor is zero. For single phase circuit, the reactive power drawn by the inductor is;
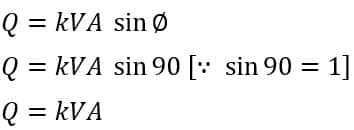
Thus, the pure inductor draws reactive power only. A similar case is with capacitors. The capacitor also draws zero active power. It draws only reactive power.
Three Phase Circuit- kW and kVA
For a three-phase circuit, the phase voltage is about 58 % of the line voltage.
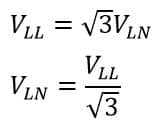
The active power(P) in a three-phase circuit is;
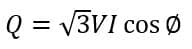
Where,
V = Line-to-line voltage
I = Line current
The reactive power(Q) in a three-phase circuit is;
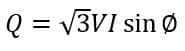
The apparent power(S) in a three-phase circuit is;
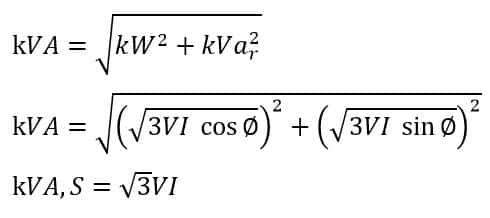
Where,
S is apparent power.
The electrical equipment always draws reactive power for equipment functioning and active power for delivering useful work. Some of the electrical equipment ratings are specified in apparent power(kVA)
The manufacturer specifies the transformer and alternator rating in kVA because he does not know at what power factor the user will operate the equipment.
Quick Comparison: kW vs kVA
| Parameter | kW (Active Power) | kVA (Apparent Power) |
| Definition | Real power consumed to do work | Total power drawn from the supply |
| Symbol | kW | kVA |
| Consumed by | Electrical devices performing actual work | All electrical devices including reactive components |
| Relationship | kW = kVA × Power Factor | kVA = kW / Power Factor |
| Example | 100 kW motor at PF 0.9 | 100 kW ÷ 0.9 ≈ 111.1 kVA |
kW to kVA Conversion Formula
The KW to KVA conversion formula is,
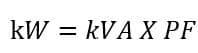
Where,
- KW- Real Power or Active Power
- KVA – Apparent Power
- PF – Power Factor
kVA to kW Conversion Formula
The KW to KVA conversion formula is,
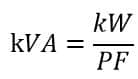
Where,
- KW- Real Power or Active Power
- KVA – Apparent Power
- PF – Power Factor
Practical Applications of kW and kVA
- Transformer & Generator Sizing: Helps select the correct kVA rating based on load and power factor.
- Motor Selection: Ensures motors are rated in kW for real work output while considering kVA for supply requirements.
- Power Factor Improvement: Identifies reactive power (kVAr) to reduce losses and optimize efficiency.
- Load Management: Differentiates between actual power consumption (kW) and total supply demand (kVA) for accurate billing and planning.
Solved problems on kW and kVA
A balanced three-phase load draws 100 KW power at a power factor of 0.90. The system line-to-line voltage is 440 Volts(RMS). What is the apparent power drawn by the load?

Line current IL

If the power factor of the system is improved to 0.995, what are the kVA and the Line current?

Line Current IL is
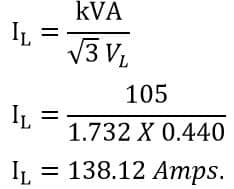
Thus, the kVA and line current decreases with the improvement of the power factor.
Thus, the kVA and kW depend on the load power factor.
Conclusion
Understanding the difference between kW and kVA is fundamental for electrical engineers and students working with AC circuits.
kW shows the real power equipment actually uses to do work, while kVA represents the total power drawn from the supply, including real and reactive power.
Recognizing the relationship between kW, kVA, and kVAr helps in accurate transformer and motor sizing, efficient load management, and effective power factor correction.
Relaated Articles:
It was really easy to understood with clear explanations.
Bundle of Thanks 😊
Can you send more samples to my email…best👏