Active Power
The power drawn by the load to do work is called the True power, Active power, or real power. When electrical energy is fed to a load, the electrical energy gets converted into other forms of energy like thermal, mechanical, or chemical. Thus, the power actually consumed by the electrical load is called active power. A heater rated 220 volts, 400 watts consumes 400 watts when 220 volts is applied to its resistance element. The 400 watts of power consumed by the heater is the real power or active power. The active power is measured in kilowatts (kW) or MW.
To calculate active power, the current flowing in phase with applied voltage is calculated.
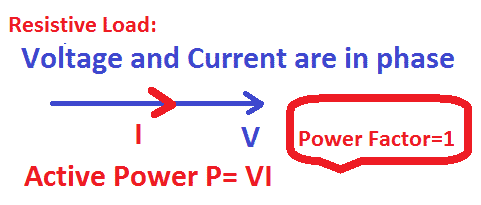
The product of the voltage and the current in phase with the voltage gives the real power or active power.
Reactive Power
Power that flows from the source to the load and from the load to the source is called reactive energy. It flows in both directions. Reactive power is measured in kilovolts ampere reactive(kVAR) or MVAR.
The inductive load causes reactance current, and thus, the current lags with the applied voltage. The capacitive load causes reactance to the applied voltage, and thus, the current leads to the applied voltage. The phase displacement between the voltage and current always exists if the load is capacitive or reactive.
The impedance offered by the capacitive and inductive loads causes power to flow back and forth from source to load and load to source. In a purely inductive circuit, the current lags the voltage by 90 electrical degrees. In a purely capacitive circuit, the current leads the voltage by 90 electrical degrees.
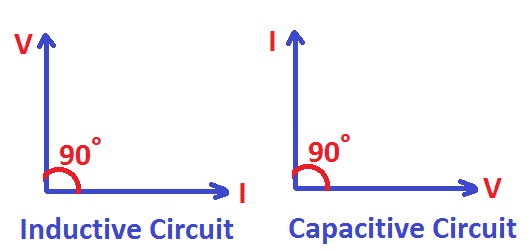
The active power in the case of the purely inductive and capacitive circuits is VICosΦ= VI Cos90=0—the reactive power in the case of purely inductive and capacitive circuits VISinΦ= VI Sin90=VI.
Apparent Power
If the load is neither purely resistive nor purely reactive, the current drawn by the load has two components of the current.
Active Component of the Current :
The current that is in phase with the applied voltage is called the active component of the current. The active or real power consumption of the load depends on the active current component of the circuit.
Reactive Component of the Current :
The current which is 90 degrees out of phase with the applied voltage is called the reactive component of current or wattless current. The reactive component of the current contributes to the reactive power.
The load whether drawing the active or reactive current, the total current of the system will increase. Therefore, the electrical system capacity is expressed in the apparent power kVA or MVA. The system needs to handle both active and reactive current, and therefore, the system is designed to take care of apparent power.
Let an electrical inductive load draw current I, and the phase displacement between voltage and current is Φ.
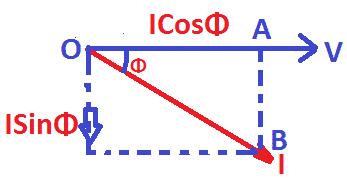
The active component of the current in phase with the voltage is ICosΦ, and the reactive component of the current component out of phase with voltage is ISinΦ. Here, CosΦ is known as the power factor.
The active, reactive, and apparent power drawn by inductive load can be calculated as follows.
Active Power of Single-Phase Load
Active power(P)
= Voltage x Current in phase with the voltage
= V x ICosΦ
= V I CosΦ
Active Power of Three-Phase Load
Active power (P)
= Voltage x Current in phase with the voltage
= √3 Vx ICosΦ
= √3 V I CosΦ
Reactive Power of Single-Phase Load
Reactive power(Q)
Q = Voltage x Current out of phase with the voltage
= V x ISinΦ
= V I SinΦ
Reactive Power of Three-phase Load
Reactive power (Q)
Q =Voltage x Current out of phase with the voltage
= √3V x ISinΦ
= √3 V I SinΦ
The apparent power is the vector sum of the active and the reactive power.
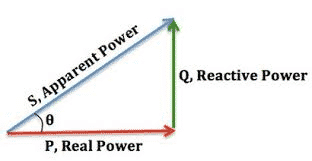
For a single-phase supply system, the apparent power drawn can be expressed by the following mathematical expression.

For a three-phase load, the apparent power is;

1 thought on “What is Active, Reactive, and Apparent Power?”