Maximum power transfer theorem is a tool for determining the condition of maximum power transfer. The maximum power transfer theorem states that the source can deliver maximum power to load if the load resistance is equal to the source resistance. The maximum power transfer theorem is applicable for AC and DC circuits. To obtain the maximum power from the source, load resistance should be equal to the source resistance. We will derive the mathematical proof of the maximum power transfer theorem and the efficiency of the system under maximum power transfer.
Explanation of Maximum Power Transfer Theorem
In the case of a DC source, it has a certain resistance. In the case of an AC source, it has a certain impedance. The source feeds current to the load. The voltage drop takes place in the source impedance when current flows through the circuit. The power lost in the source resistance must be minimum to get the maximum power delivery of the source.
If the power loss in the source resistance is greater, the maximum power delivery from the source can not be ensured. There is a certain relationship between the source impedance and load impedance for which maximum power delivery from the source can be achieved. The maximum power theorem states that if the load resistance is equal to the source resistance, the maximum power will be delivered by the source.
The source resistance is the resistance viewed from the load side, and we can find its value using the Thevenin theorem. Therefore, the source resistance is also called Thevenin resistance. We take the DC circuit to understand the maximum power transfer theorem.
Thevenins Equivalent Circuit
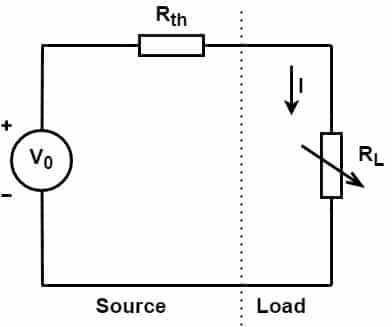
In the above Thevenin Equivalent circuit, the maximum power transfer theorem states that “the maximum amount of power will be delivered in the load resistance if the load resistance is equal to the Thevenin or Norton source resistance.
The source resistance viewed from the load side is Rth, and the Thevenin voltage is V0. According to the maximum power transfer theorem, the maximum power transfer occurs when the source resistance is equal to the load resistance.
Rth = RL
Maximum Power Transfer Example – 1
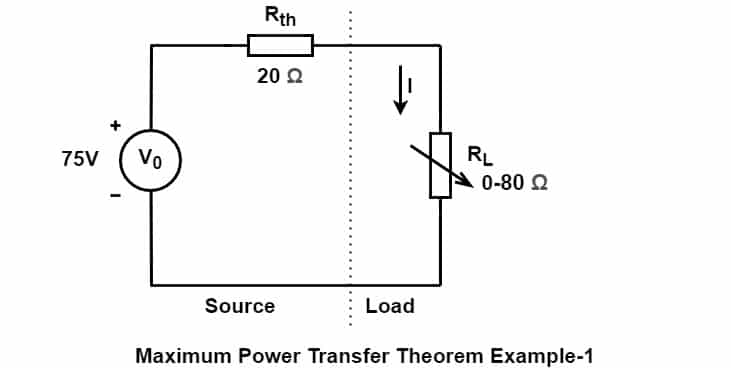
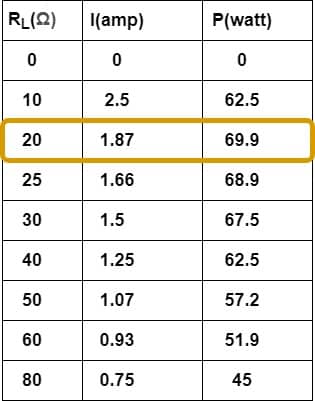
According to the maximum power transfer theorem, the source delivers maximum power to the load if the value of load resistance is equal to the source resistance. The value of the load resistance should be 20 Ω. Now, let us verify this statement by calculating the power consumed by the load at various load settings.
Maximum Power Transfer Theorem Proof
We take the following DC circuit to derive the condition of maximum power transfer.

The DC source supply current to the load. The power dissipation in the load resistor RL is P= I2R. The current I flowing through the circuit is:
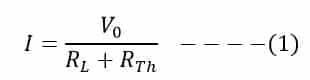
The power dissipation in the resistor RL is:

Putting the value of I from equation (1) in equation(2), we get:
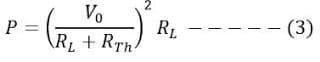
The maximum power delivery is possible if;
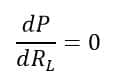
Equation(3) can be solved as follows.
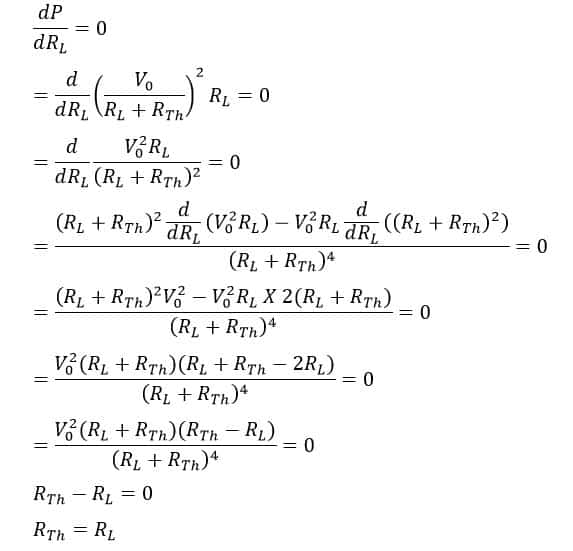
Thus, the condition for maximum power transfer is that the source delivers maximum power to the load if the source resistance is equal to the load resistance. Now, we will calculate the system efficiency under maximum power transfer conditions.
Efficiency of Maximum Power Transfer
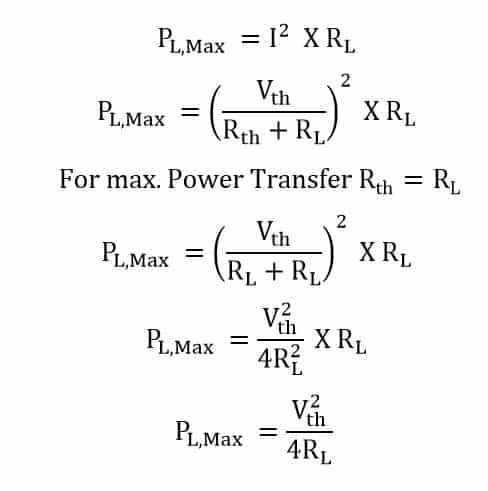
To calculate the efficiency, we first calculate the maximum power transfer when the load resistance is equal to the source resistance.
Maximum Power Delivered to the Load

Total power transferred from the source is:
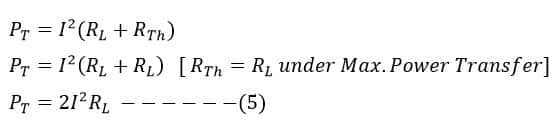
We can calculate the maximum efficiency by Dividing equation(4) and equation(5)
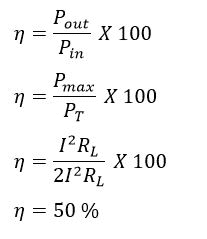
Hence, the efficiency is 50% at the condition of maximum power transfer. At maximum power transfer conditions, the source delivers 50 % of the generated power to the load, and at other conditions, the source drives a small percentage of power to the load.
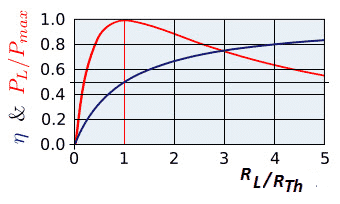
Maximum Power Transfer Formula
The fundamental formula for the Maximum Power Transfer is’
Application of Maximum Power Transfer Theorem
The efficiency of the electrical system is 50 % when the load resistance is equal to the source resistance. It means the source delivers 50 % of power to the load, and the remaining 50% of power is lost in the circuit. The MPTT is not applicable where a large power transfer is taking place. In view of this, MPTT is not applicable for power transmission. In communication circuits, the magnitude of power transfer is very small, and low efficiency is not a problem in communication circuits. The maximum power transfer theorem has tremendous applications in communication circuits for impedance matching.
Wow. You described well. Especially that tabular example.