The voltage source supplies current to the electrical circuit. When the load is connected across the voltage source, the voltage source supplies current to the load.
Ideal Voltage Source
An ideal voltage source is capable to maintain the constant voltage across its terminals. The voltage across the voltage source terminals remains constant, and the voltage is independent of the current. The symbol of the voltage source is given below.
The voltage across the terminals of an ideal voltage source remains constant, and the voltage does not drop with an increase in the circuit current. The voltage across an ideal voltage source with a change in the circuit current is depicted below.
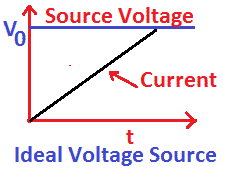
The voltage of an ideal voltage source remains constant if there is no voltage drop across its internal resistance. A voltage source has a certain resistance, which causes a voltage drop across its internal resistance. An ideal voltage source must have zero internal resistance. In this condition, the voltage across the load will be equal to the voltage across the terminals of the voltage source.
Internal resistance of an Ideal Voltage Source
An ideal voltage source is capable of maintaining a constant voltage across its terminal from a no-load to a full-load condition. An ideal source circuit is given below.
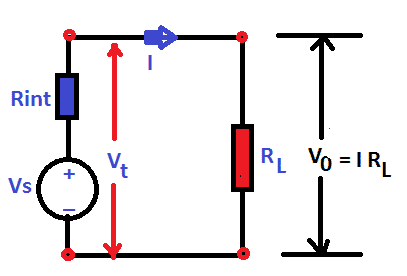
An ideal voltage source voltage across the load(Vo) is equal to the voltage across the terminal voltage(Vt).
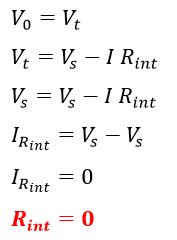
Thus, the internal resistance of an ideal voltage source is zero. The source voltage is equal to the voltage across the load, and no voltage drop takes place in the internal resistance because an ideal voltage source has zero internal resistance.
Practical Voltage Source
The internal resistance of an ideal voltage source is zero. However, a practical voltage source has some internal resistance. The symbol of the practical voltage source is depicted below.
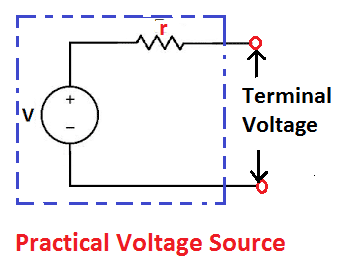
The internal resistance (r) of an ideal voltage source is zero. However, practically, the voltage source has some internal resistance. The symbol of the practical voltage source is depicted below.
The terminal voltage at the source when current is delivered to the load no longer remains constant, and the voltage at the source terminal is somewhat less than the terminal voltage at no load condition. The practical voltage source at load condition is depicted below.
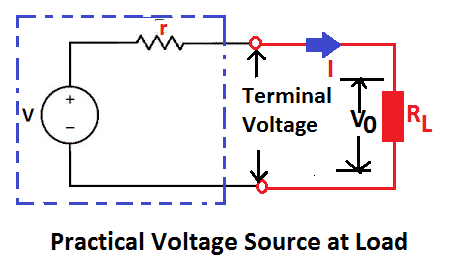
The voltage across the load can be found by applying Kirchoff’s voltage law (KVL). According to KVL, the algebraic sum of the voltages in a loop is equal to zero.
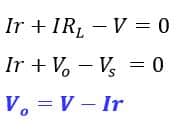
The voltage across the load can not be equal to the source voltage when the current is delivered by the voltage source. The difference in the voltage across the load and the source voltage depends on the magnitude of the current flowing in the circuit. The voltage across the load is equal to the source voltage minus the voltage drop in internal resistance. The higher the circuit current, the more voltage drops in the internal resistance and the voltage across the load will drop accordingly. The same is shown in the graph below.
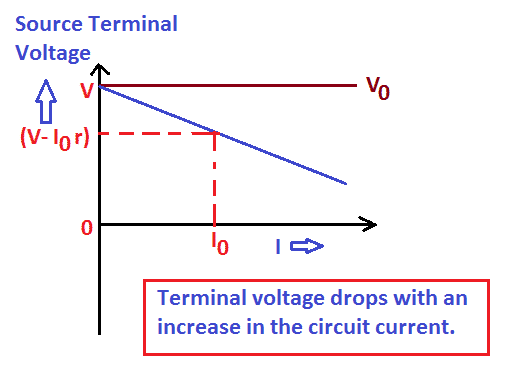
When the voltage source delivers current, the voltage across the load can not be equal to the source voltage. The difference between the voltage across the load and the source voltage depends on the magnitude of the current flowing in the circuit.