In this article, we will discuss the condition for which the induction motor delivers the maximum torque. The torque of an induction motor depends on the rotor current, rotor power factor, and stator flux per pole. The rotor current further depends on the slip, rotor resistance, and rotor reactance. Thus, we can say the torque of an induction motor depends on the followings.
- Stator flux/pole
- Rotor resistance
- Rotor reactance
- slip
The rotor resistance, slip, and rotor reactance causes the power factor of an induction motor to vary. Thus, in simple terms, the torque of an induction motor depends on stator flux, rotor current, and the rotor power factor.
Running Torque of Induction Motor
The running torque of an induction motor can be expressed by following the mathematical formula.

From the above mathematical expression of the running torque of an induction motor, the following conclusions can be made.
- At slip(s) = 0, Torque(T) = 0
- At normal speed, slip is small so sX2 is negligible as compared to R2. Therefore, the torque is directly proportional to the slip.
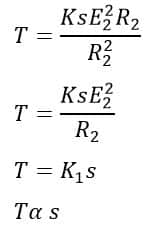
- When the slip increases beyond full-load slip, the torque increases and becomes maximum at a particular point The maximum torque in an induction motor is called pull-out or break-down torque. Its value is generally twice the full-load value when the motor operates at rated voltage and frequency. With a higher value of slip, The term 𝑠2𝑋22 rapidly increases with a higher value of the slip and this term becomes significant in the torque equation. In comparison to this term, 𝑅22 is very small and may be neglected. Thus the torque in this condition is inversely proportional to slip.
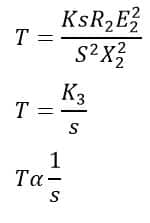
The above points may also be understood by the torque slip characteristics of the induction motor.
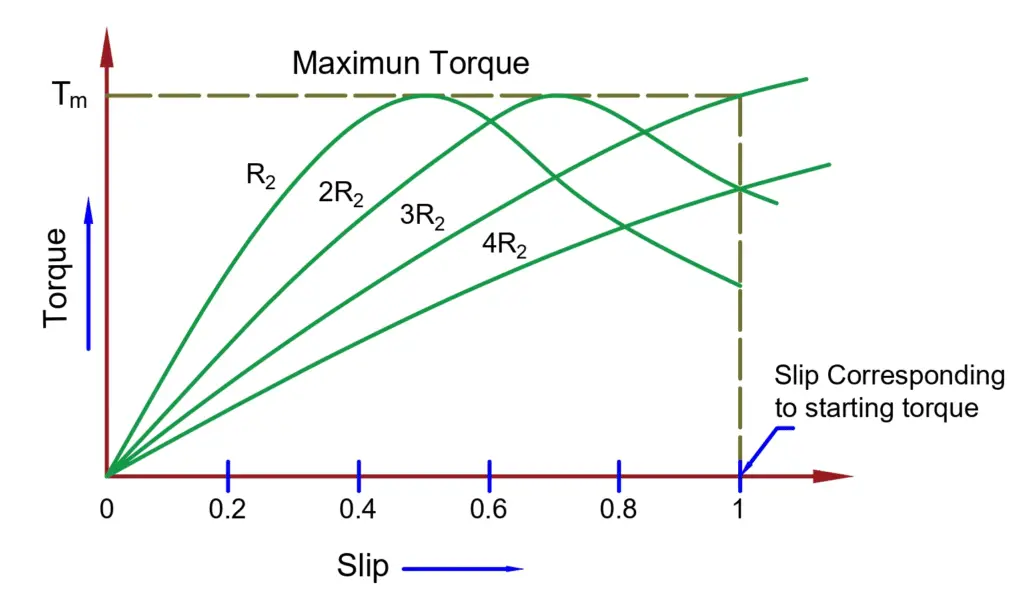
- At the start, the slip is 1 and T=0
- Up to pull-up torque, the torque is proportional to slip.
- After the point of pull-up torque, the torque is inversely proportional to the slip.
Maximum Torque Condition of an Induction Motor :
The torque equation of the induction motor is;
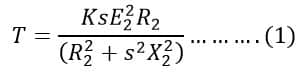
The equation(1) can be written as;
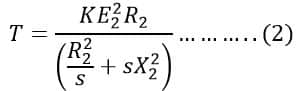
The denominator of equation(2) can be written in the square form,
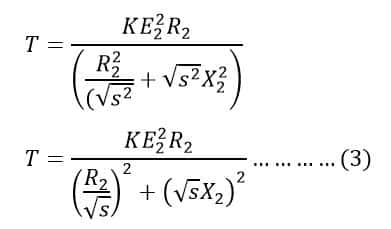
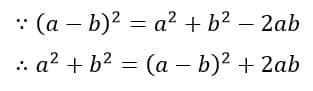
Applying the above property in equation(3). we get;
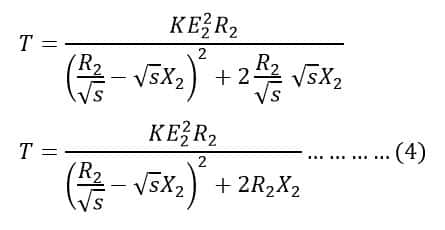
The developed torque will be maximum if the value of the right-hand side of equation (4) is maximum. This condition is possible if the value of the denominator shown below is equal to zero.
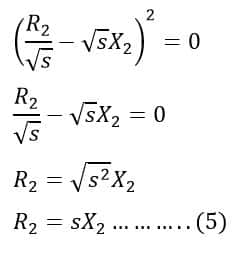
Therefore, the developed torque of an induction motor is maximum if the rotor resistance per phase is equal to the rotor reactance per phase under running conditions.
Alternate method to derive Condition for Maximum Running Torque of Induction Motor
The expression for the torque of an induction motor under the running condition is given as,
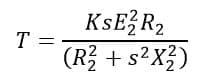
The E2, R2, X2, and k parameters are constants, and slip s is only the variable. The slip changes as the load on the motor changes. Hence, the slip is the deciding factor of the torque produced by the motor. Thus, the torque of the induction motor depends on the slip. The torque produced by an induction motor is maximum if the differentiation of the torque with respect to the slip is equal to zero.
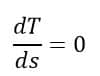
Putting the value of “T” in the above equation,

Therefore,
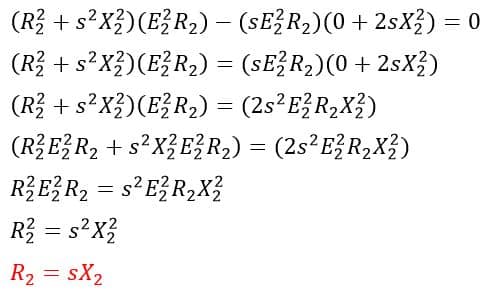
The slip at which the torque is maximum is denoted as sm.
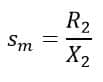
The maximum slip is the ratio of standstill per values of resistance and reactance of the rotor when the motor produces maximum torque.
Expression for Maximum Torque
The maximum torque of an induction motor can be obtained by substituting the maximum slip value(sm = R2/X2 )in the torque equation.
The torque equation is
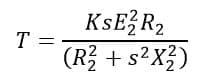
Substituting R2 = sX2 in the above torque equation,
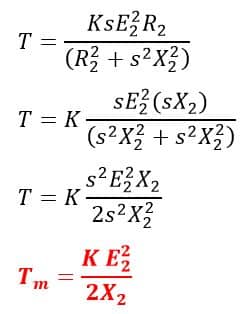
From the above equation, it is clear that the maximum torque is independent of the rotor resistance.
The speed of the motor is;

The below equation shows the rotor speed at the maximum torque.
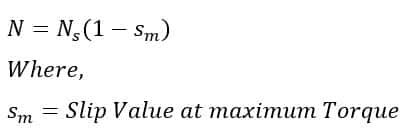
Conclusion about Maximum Torque of Induction Motor
From the above discussions, we can make the following conclusions.
- The maximum torque does not depend on the rotor circuit resistance.
- The standstill reactance of the rotor circuit plays a vital role in maximum torque. The maximum torque produced by the motor is inversely proportional to the standstill reactance of the rotor. Hence, the inductance of the rotor must be kept as small as possible.
- The maximum torque is directly proportional to the square of the standstill rotor-induced emf(E2).
- By inserting resistance into the rotor circuit and varying the resistance, it is possible to obtain the maximum torque at any desired slip or speed.
To develop maximum torque at the start of the induction motor, the rotor resistance must be high and should be equal to rotor reactance(X2). When the motor starts accelerating, the value of the resistance must be reduced to obtain torque in running conditions.
Solved Problem
The rotor resistance and reactance of a 440 V, 6 poles, 3 phase, 50 Hz star connected induction motor is 0.02 and 0.15 Ω respectively. Calculate the followings.
(1)Starting torque
(2) slip at which maximum torque will occur
(3) speed at which maximum torque will occur
(4) maximum torque
(5) full load torque if full load slip is 4 %. Assume the ratio of the stator to the rotor turns as 4.
Given Data-
P = 6
Ns= 120f/P
Ns= 120 X 50/6
Ns= 1000 rpm
N= 16.66 rps
R2= 0.02 Ω
X2 =0.15 Ω
Line Voltage= 440 Volts, Motor is star connected therefore, the phase voltage is;
= 440/√3 = 254 V
Transformation Ratio(K)= Rotor turns/stator turns
K= 1/4 =0.25
Also,
Transformation Ratio= Rotor Voltage/Stator Voltage
0.25 = E2/E1
E2 = 0.25 X 254
E2= 63.5 Volts
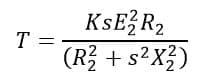
(1) At the start, the slip of the motor is unity.
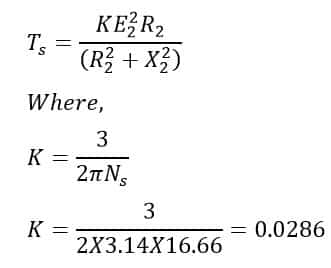
Therefore, the starting torque of the induction motor is;

(2) slip at maximum torque
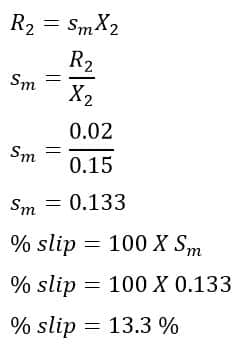
(3) Speed at which maximum torque will occur
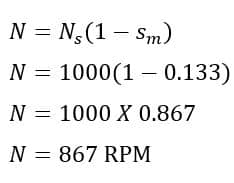
(4) Maximum torque
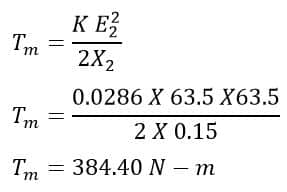
(5) Full load torque if full load slip is 4 %.
s= 0.04
