We can calculate the electric power by multiplying the voltage and current. When we apply voltage to an electric circuit, the circuit draws current. The magnitude of electric current depends on the voltage and the impedance of the circuit.
Ohm’s Law to Determine Current
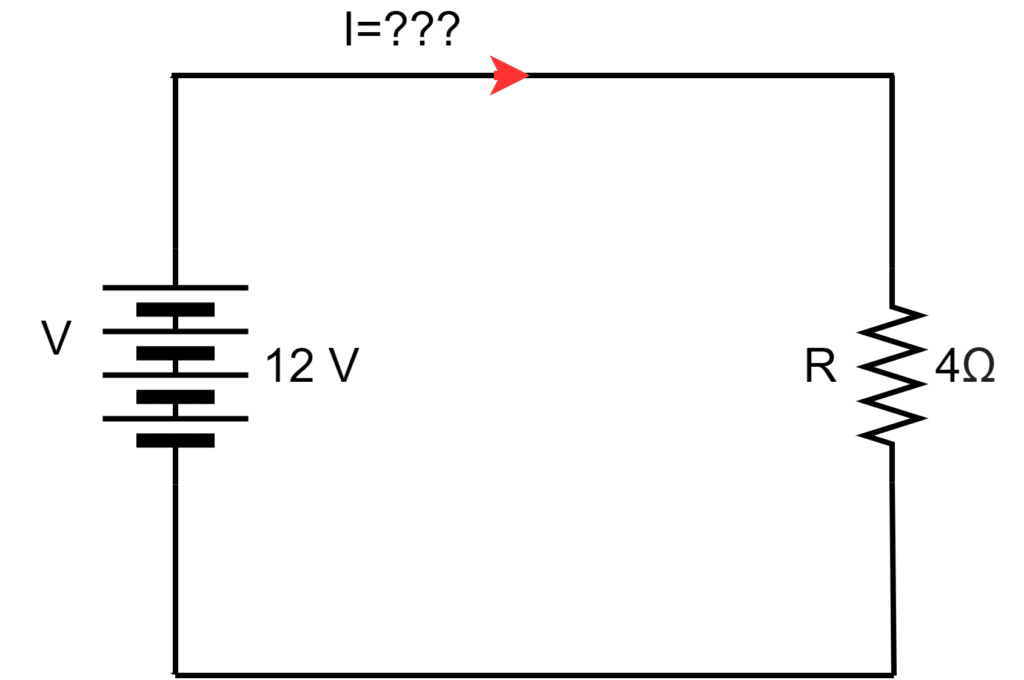
If we observe the above circuit, the voltage and the circuit resistance are known. The current flowing in the electric circuit can be determined using Ohm’s law.

Thus, the current in the above circuit is;
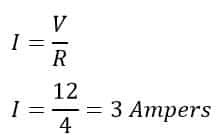
Now we know the value of electric current. If we multiply this current value by voltage, we get a power equation and with this equation, we can calculate the electric power using this power equation. The product of these two quantities is the power consumed by the electric circuit.
Power Formula
The formula of power is given below.
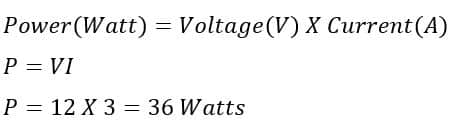
The electric power drawn by the circuit is 36 Watts. In other words, this electric power is the heat that dissipates through the resistor.
Observation- The power drawn by the circuit depends on the magnitude of the voltage and the resistance. If we keep the resistance constant and vary the voltage, the power in the circuit will increase. The increase in the power of the circuit happens because of two reasons.
- Increase in voltage
- Increase in current because of voltage increase
Thus, the voltage is the driving force for the current, and we can say that the reason for increased power is only the voltage under the condition the resistance of the circuit is constant.
Now, we will discuss how power increases with an increase in voltage.
Power with Increasing the Battery’s Voltage
On increasing the voltage, the current will increase. Here we consider that the resistance of the circuit is not changing and it is fixed.
Again, we take the same case of the battery connected to a resistive circuit. We have seen that the circuit’s power is 36 Watts when the battery voltage is 12 volts and the current is 3 amperes.
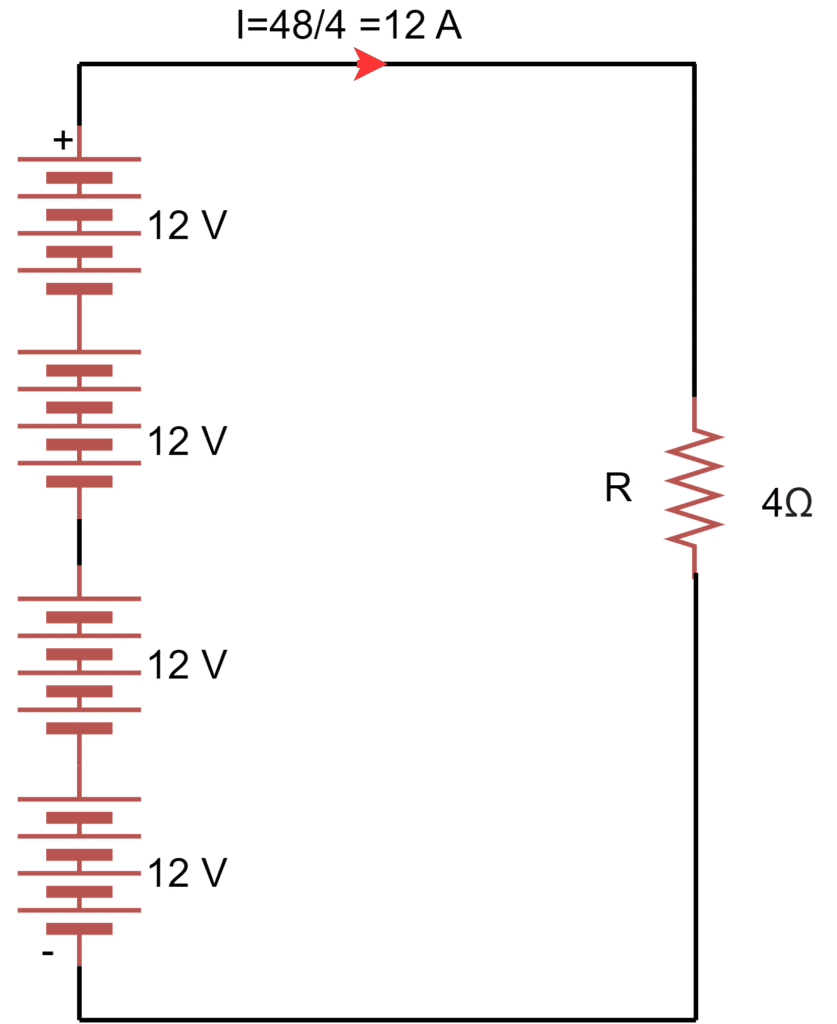
Now, we connect one more battery of 12 volts in the series with the existing 12 volts battery, then the total voltage is 24 volts. The 24 volts supply is fed to the same circuit resistance of 4 ohms.
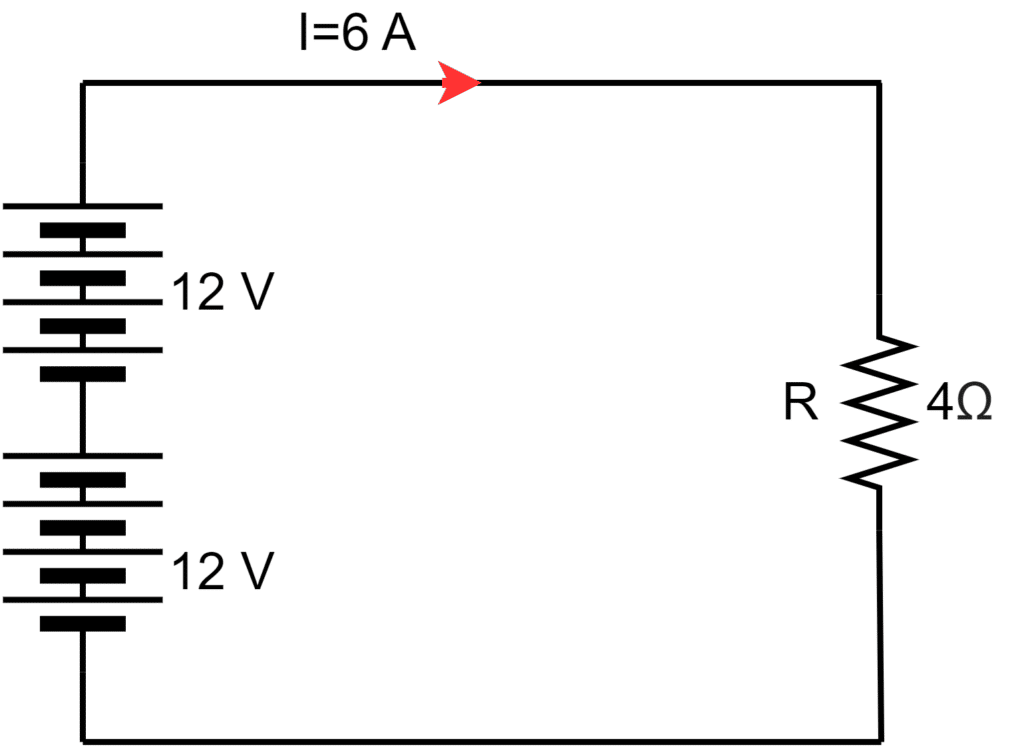
The current is the circuit will be;
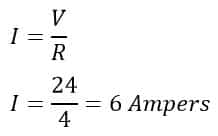
We can calculate the electric power using the following formula.
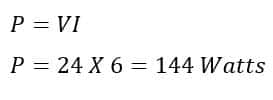
Relationship between the Voltage and Power
Now, we tabulate the voltage and power to understand the increase in power by Increasing a battery’s voltage.
| Battery Voltage(V) | Power(Watt) |
| 12 | 36 |
| 24 | 144 |
If we observe the readings, we will find that on doubling the voltage, the power increases to 4 times when resistance is fixed. We can substantiate this relationship with ohm’s law.
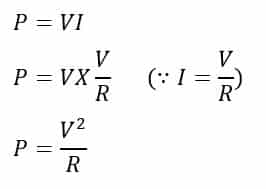
From the above equation, it is clear that the power consumed by the circuit is proportional to the square of the voltage when the resistance is fixed.
Now, you can easily calculate the power referring to the above concept. The power of the circuit is 36 watts when the voltage is 12 volts. Now, calculate the power when the voltage is 48 volts.
An increase in the voltage from its initial value is;
= 48/12 = 4 times
The power increase is proportional to the square of the voltage, so now power will be;
P= (4)2 X 36
P= 576 Watts
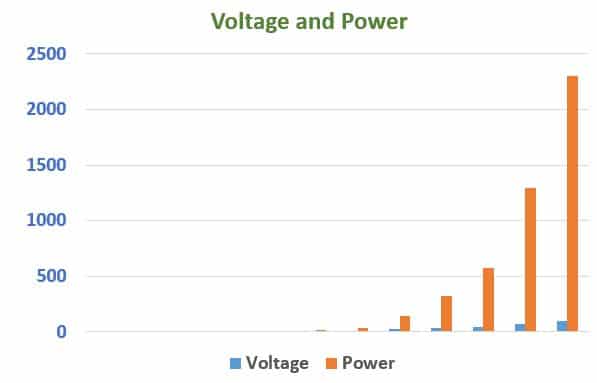
Table showing voltage and corresponding power when resistance value is fixed.
| Voltage(V) | Power(Watts) |
| 1 | 0.25 |
| 2 | 1 |
| 3 | 2.25 |
| 4 | 4 |
| 5 | 6.25 |
| 8 | 16 |
| 12 | 36 |
| 24 | 144 |
| 36 | 324 |
| 48 | 576 |
| 72 | 1296 |
| 96 | 2304 |
If we draw a graph between the voltage and the power when resistance is kept constant, the graph will be like this;
Relationship between the Current and Power
We can calculate the power if the current and resistance is known. The relationship between current and power can be established using Ohm’s law.
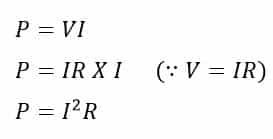
Joule’s Law Vs. Ohm’s Law
James Prescott Joule first discovered the mathematical relationship between power dissipation and current through the resistance. He formed the power equation (P = I2R), which is properly known as Joule’s Law.
The power equation is so closely related to Ohm’s law.
Power Equations for Electric power calculations
The followings are the power equations.
