The magnetic lines of forces follow a closed path. This closed path is called the magnetic circuit. In an electric circuit, the current follows a closed path. In a similar way, the flux follows a closed path in the magnetic circuit. Thus, the magnetic flux lines start from one end and meet at the same point after completing the closed path.
We can generate the magnetic flux by two methods. They are ;
- Permanent magnet
- Electromagnet
It is possible to generate flux in the magnetic circuit by a permanent magnet or electromagnet.
The first requirement for flux generation is the presence of a magnetomotive force generator in the magnetic circuit. The MMF is a basic driving force responsible for setting up magnetic flux. The flux in the magnetic circuit depends on the MMF and the reluctance of the magnetic circuit. It is desirable that the magnetic circuit must have the least reluctance for better performance. Magnetic material such as iron, steel, CRGO has low reluctance & higher permeance.
The operation of the electric motor, transformer, electromagnetic relay is not possible without the use of a magnetic circuit.
To understand the concept, we take an example of an N turns coil wound on a magnetic core. When current I flows in the coil it produces a flux (ø) that flows in the closed path in a magnetic circuit. The magnitude of the flux depends on the coil current, coil number of turns, and the reluctance of the magnetic circuit.
Magnetic Flux in a magnetic circuit
Consider a solenoid having N turns wound on an iron core. The magnetic flux ( ø Webers) sets up in the core when the current of I ampere flows in a solenoid coil.
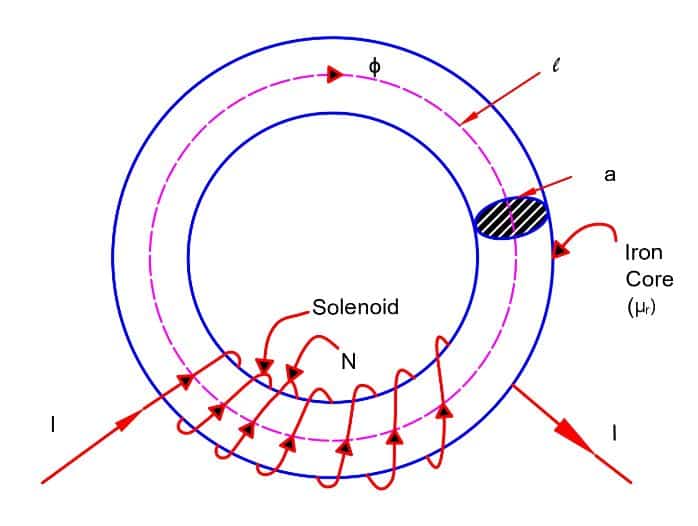
Let,
ℓ = mean length
A = cross-sectional area of the core
µr = relative permeability of the core
I = current flowing in the coil
H= Magnetic field intensity
Now the flux in the core can be calculated as follows.
Flux in the core = Flux density x Cross Sectional area of the core
Flux in the core = Flux density x Cross Sectional area of the core
ø = B A ———–(1)
( Also, B = μ0 μr H )
ø = μ0 μr H A ———–(2)
ø = (μ0 μr A)H ———–(3)
( H = NI/ℓ)
ø = (μ0 μr A)NI/ℓ ———–(3)
ø = NI/(ℓ /μ0 μr A) ——–(4)
( Here (ℓ /μ0 μr A) is the reluctance of the magnetic circuit Rm.
ø = NI/Rm ——–(5) ( Where reluctance Rm = ℓ /(μ0 μr A)
From equations (4) &(5) we can conclude that the magnetic flux is
- Directly proportional to the number of turns
- Directly proportional to the current
- Inversely proportional to the reluctance
Read Next: