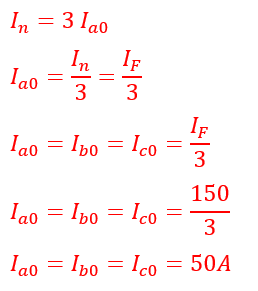Definition: During an earth fault in an electrical circuit, an unbalanced current flows. This current is also referred to as the zero sequence current or the DC component of the fault current. When all three phases have no phase displacement, it is called the zero phase sequence. The zero sequence current can be represented by three vector lines, which can be calculated by adding the vector of the three phases current. The equation below expresses the zero-phase sequence current.
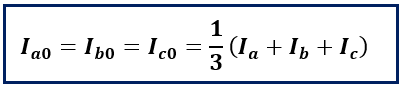
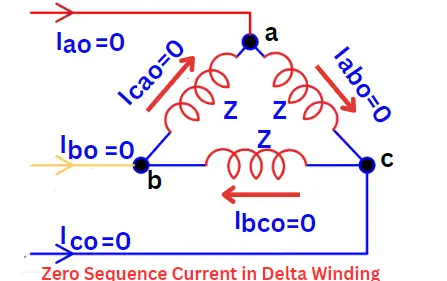
Zero Sequence Current in Delta-Connected Winding
The diagram provided below depicts the delta-connected winding. In this type of connection, the zero sequence current flowing through phases a, b, and c has the same magnitude and phase. As shown in the figure, this current circulates in the phase windings of the delta connection. The presence of zero sequence voltage gives rise to these zero sequence currents.
Node “a: current,
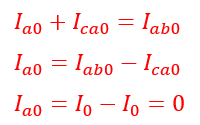
Node “b” current.
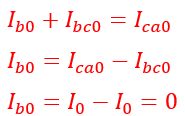
Current at node c,
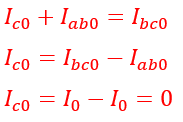
The delta connection eliminates zero sequence current as there are no return paths for such current.
In a delta-connected circuit, the circuit’s impedance becomes infinite when there is no return path for the zero sequence current in the line. This is due to the lack of a return path for the zero sequence current. The open circuit at point P in the single-phase equivalent zero sequence network represents this infinite impedance with a zero sequence impedance Z0.
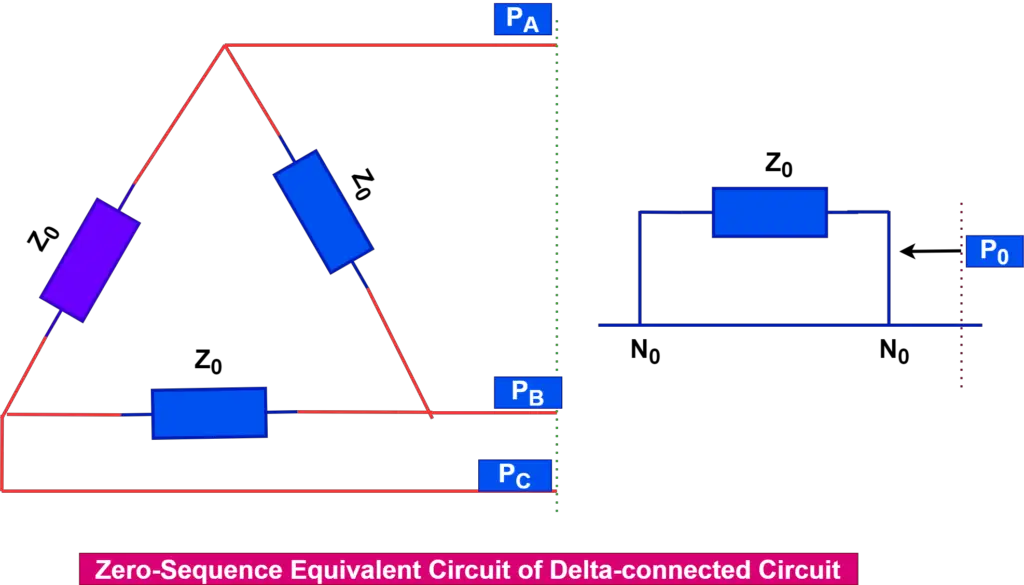
There is a closed path for zero sequence current in the delta circuit, and we represent it by connecting zero sequence impedance Z0 to the current.
Zero Sequence Current in Star-Connected Winding with Neutral Isolated from Ground
Let’s consider a star-shaped winding that doesn’t have a neutral return. This is shown in the figure below.
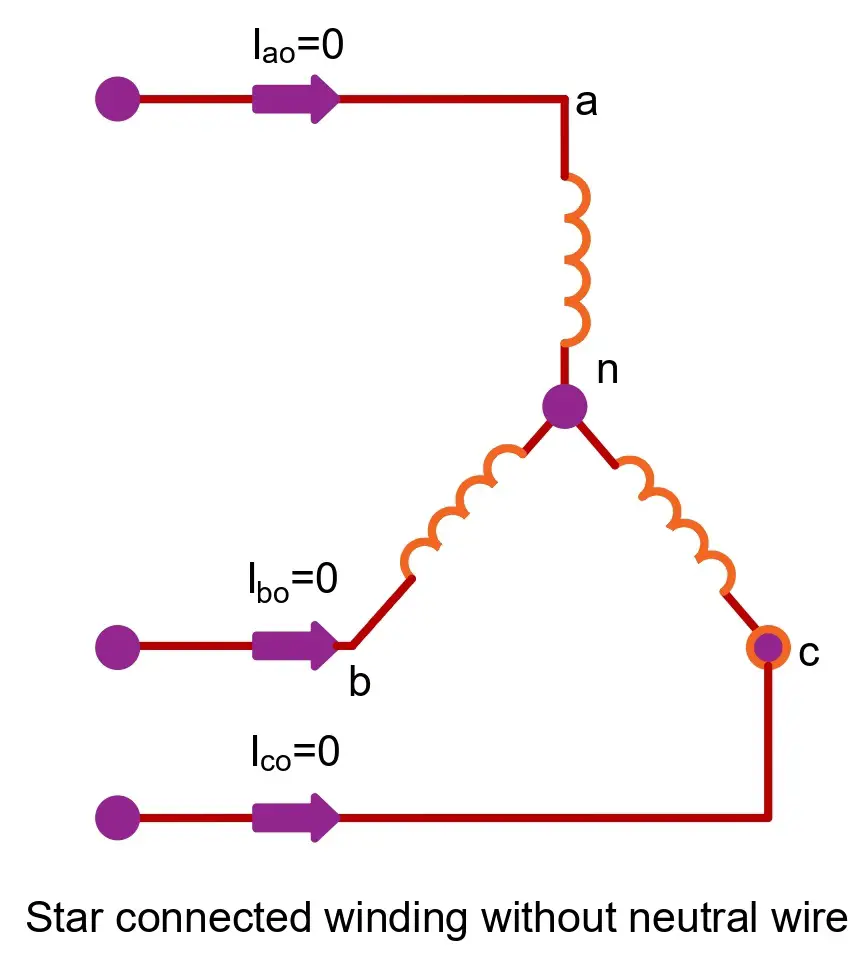
In this case,
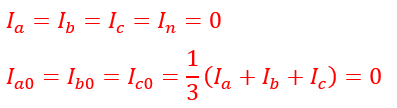
In a three-wire system without a neutral return, the equation indicates a zero sequence current.
Zero Sequence Current in Star-Connected Winding Without Neutral Return
The diagram below illustrates a winding connected in a star configuration and grounded at the neutral point.
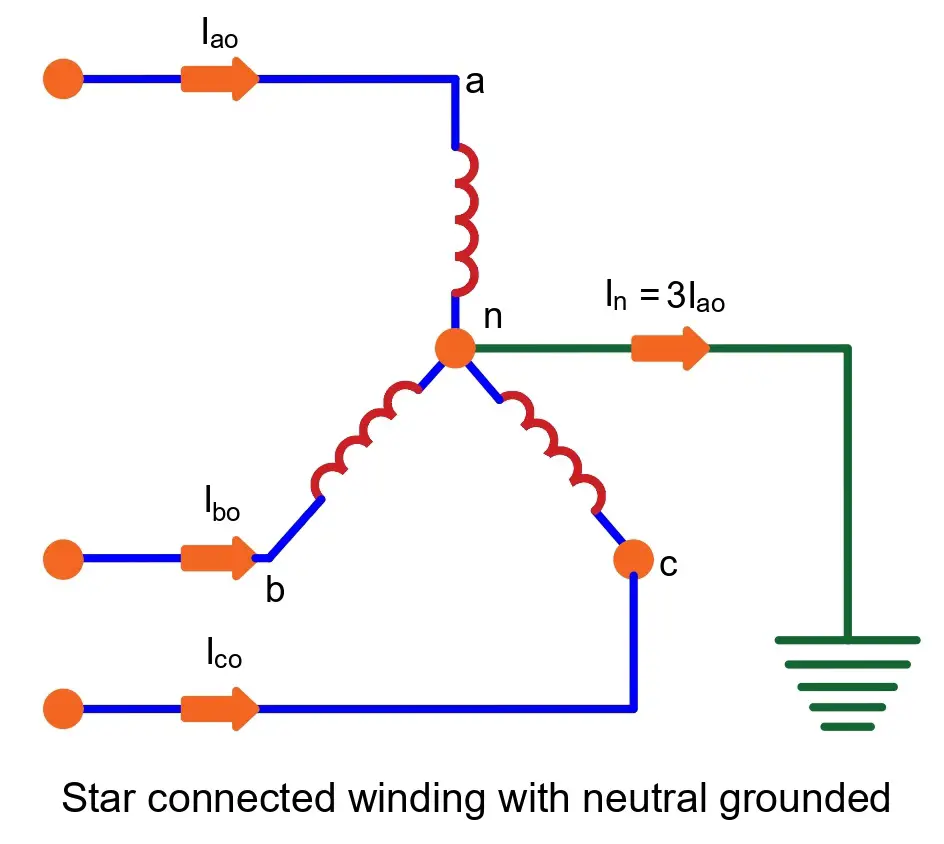
Here,
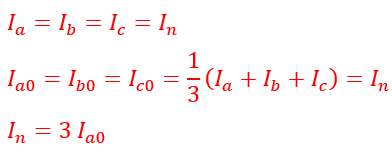
The zero sequence current in a three-phase grounded system flows from the phase winding and the lines, as shown in the above equation.
Solved Example
The fault current during a line-to-ground fault in the faulted phase is 150 amperes. Calculate the zero sequence current.
Solution:
All the sequence currents are equal in line-to-ground(L-G) faults.