Line voltage and phase voltage are widely used terms in a three-phase power system. The voltage or potential difference between any two phases’ is called the line voltage. It is denoted by Vline or VL-L. The potential difference between the phase and neutral is called the phase voltage, and it is denoted by VP.
In a three-phase system, there are three conductors that form a three-phase system. If the voltage of phases is R, Y, and B,( Red, Yellow, and Blue), then the line voltage VRY is equal to the potential difference between the R and Y phases. Similarly, the line voltage VYB is equal to the potential difference between the Y and B phases.
The star connection is used where we need to implement a 3-phase 4-wire system to get neutral for single-phase loads, and the delta connection is used where we need to design a 3-phase 3-wire system. Both systems have different current and voltage relationships between their phases and lines.
In this article, we will derive the expressions to establish the relationship between line and phase voltages in star and delta connections.
What is a Star Connected System?
An electrical system in which winding or phases of the system are connected in a star or Y-Configuration is referred to as a star-connected system. It is also known as a Y-connected system.
In a star-connected system, one end of all the phase windings is joined together and the other ends of the phase windings are taken out as line terminals. A typical star connection is shown in the following figure.
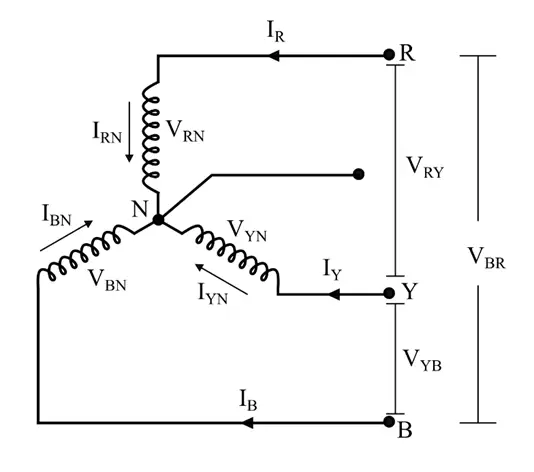
It has three phase windings namely R, Y, and B respectively. The common point of the three windings is termed neutral (N).
Relationship between Line and Phase Voltages in Star Connection
In the start connected system shown in the above figure, it is clear that the phase winding is connected in series with the line. Therefore, the currents flowing through the phase windings and lines of the system are the same.
Consider a star-connected system with phases marked as VRN, VYN, and VBN. The line voltages are marked as VRY, VYB, and VBR.
Since, we have considered that the system is balanced, therefore,
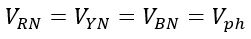
And
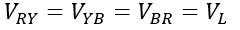
Here, Vph is the phase voltage
and, VL is the line voltage.
From the circuit diagram, it is clear that the phase-to-phase voltages and phase voltages are not equal. Instead, the line voltages are equal to the phasor sum of phase voltage between two adjacent phases.
Now, let us derive the relationship between the line and phase voltage of this star-connected system. For this, we will first draw a phasor diagram of the given star-connected system which is shown in the following figure.
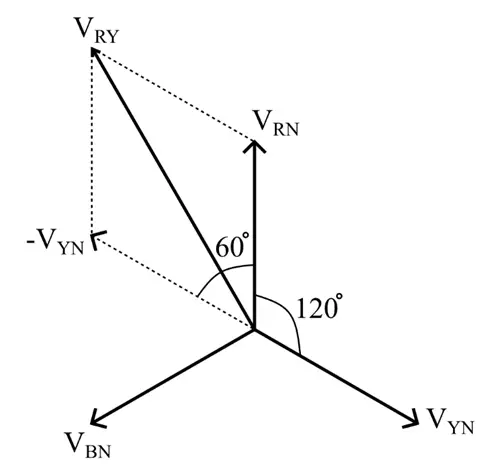
Here, we will make calculations only for one phase and line because the system is balanced. Thus, the relationship between the rest two phases and lines will be the same.
In the circuit diagram, we have,
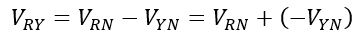
Since the phase angle between VRN and VYN is 120° electrical (balanced star connection). Therefore, the angle between VRN and -VYN will be 180° – 120° = 60° electrical.
Hence, the magnitude of the line voltage VRY will be,
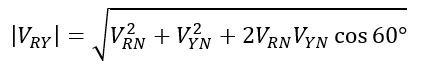
We know,
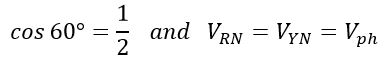
Therefore,
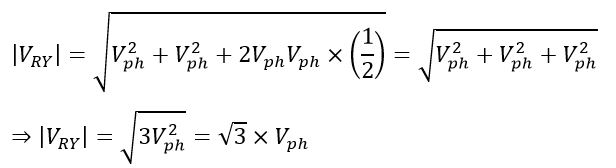
Since VRY = VL, Therefore, in a star-connected system,
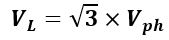
In other words, the line voltage is √3 times the phase voltage.
Similarly, for VYB and VBR, we the same result.
Relationship between Line and Phase Voltages in Delta Connection
In the delta connection, the starting end of three-phase coils is connected to the endpoints of the coil. Both ends of a coil are denoted as the start and finish coil. The finish end of one coil is connected to the start point of the second coil, and the finish end of the second coil is connected to the start point of the third coil. finally, the finish end of the third coil is connected to the start point of the first coil. Thus, the circuit forms like a closed mesh. The coils connected in the delta connection are shown below.
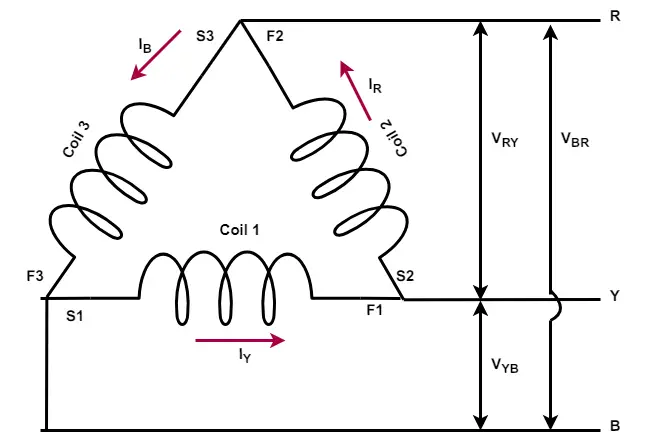
The delta-connected system does not have a neutral point, and therefore the line voltage is equal to the phase voltage.
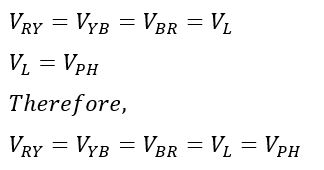
Difference between Line Voltage and Phase Voltage
| S.N | Line Voltage | Phase Voltage |
| 1. | The line voltage is √3 times the phase voltage in the star connection. Thus, the line voltage is 173 % of the line voltage. | Line voltage is more than the phase voltage in the star connection. If the phase voltage is 240 V, then the line voltage will be √3 X 240= 415 volts. |
| 2. | Line voltage is the potential difference between two phases.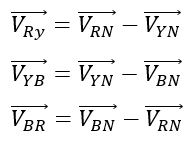 | Phase voltage is the potential difference between phases and neutral.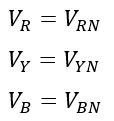 |
| 3. | Phase voltage is less than the line voltage in the star connection. If the line voltage is 440V, then the phase voltage will be 440/√3= 254 volts. | Line voltage is equal to the phase voltage in the delta connection. |
| 4. | Phase voltage is equal to the line voltage in the delta connection. | Phase voltage is equal to the line voltage in delta connection. |
Solved Examples
Example-1: In a star-connected system, the line voltage is 440 volts. Calculate the phase voltage.
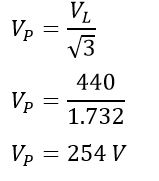
Example-2: In a star-connected system, the phase voltage is 240 volts. Calculate the line voltage.
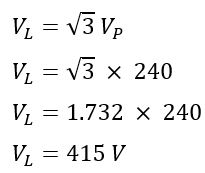
Example-3: In a delta-connected system, the line voltage is 440 volts. Calculate the phase voltage.

Conclusion
In conclusion, in a star-connected system, the line voltage is √3 times the phase voltage. However, the line current and phase current are equal. In the delta connection, the phase voltage is equal to the line voltage. But, and line current is √3 times of phase current.
The star-connected system is widely used in electrical systems where the neutral wire is required like in generating plants and distribution systems to supply single-phase and three-phase loads.