Definition: The Series Magnetic Circuit refers to a magnetic circuit consisting of various parts made of different materials and with varying dimensions, all carrying the same magnetic field. To understand the concept of a series magnetic circuit, it is important first to understand the basics of what a magnetic circuit is and its reluctance.
What is a Magnetic Circuit?
The magnetic flux follows a certain closed path in a magnetic material. Thus, the magnetic circuit is a closed path that magnetic flux follows. It is similar to how an electrical circuit provides a path for the flow of electric current. Magnetic materials such as iron cores and coils are the components of a magnetic circuit. You can analyze the behaviors of a magnetic circuit using Ohm’s Law and Kirchhoff’s Law, which are applicable to electrical circuits.
Thus, a magnetic circuit is analogous to an electrical circuit, and magnetic flux is analogous to an electric current.
You may read this article to learn more about– Magnetic circuit
What is a Magnetic Reluctance?
The property of the materials and components in a magnetic circuit that offers opposition to the establishment of magnetic flux is known as magnetic reluctance. Magnetic reluctance is analogous to electrical resistance in an electrical circuit. The reluctance of the magnetic circuit opposes the flux, and the electrical resistance opposes the flow of electric current.
You may read this article to learn more about– Magnetic Reluctance.
Series Magnetic Circuit Explanation
Let’s take a composite magnetic circuit made up of three types of magnetic materials with different permeabilities and lengths and an air gap with a permeability (μr ) of 1. Each path in the circuit has its own reluctance. The series magnetic circuit diagram is shown below.
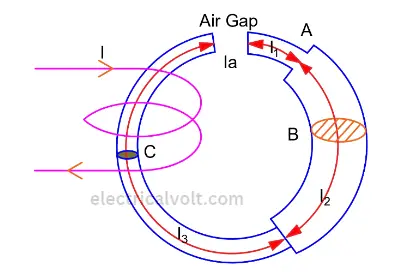
Current I is passed through the solenoid having N number of turns wound on the one section of the circular coil. Φ is the flux set up in the core of the coil.
One section of the magnetic circuit has a circular coil with N turns. When a current I passes through the solenoid, it generates a flux Φ in the core of the magnetic material.
The total reluctance of the circuit is the sum of the individual reluctances of each path, as they are connected in series.

We know,
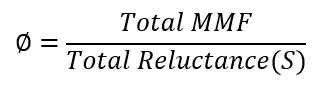
Therefore,
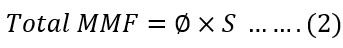
Putting the value of reluctance (S) from equation 1 in equation 2, we get
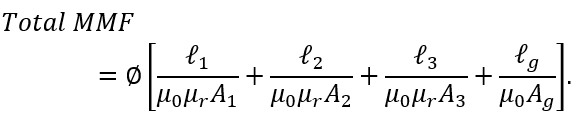
Since φ=BA, putting the value of flux(φ) in above equation, we get;
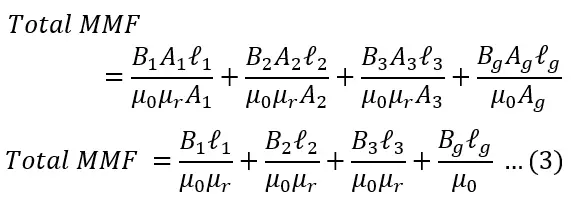
Since.
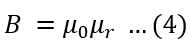
Putting the value of B from equation 4 in equation 3,
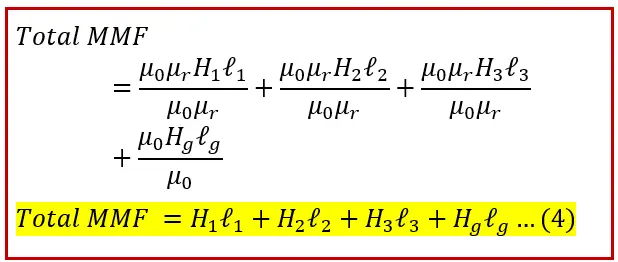
Procedure for the Calculation of the total MMF of a Series Magnetic Circuit
By following the steps below, you can calculate the total MMF in a series of magnetic circuits.
- List down all the magnetic elements in the series circuit. These could be cores of transformers, coils, or any other magnetic devices.
- Find the value of the different sections’ flux density (B). As we know, B = φ/a where φ is the flux in Weber, and a is the area of the cross-section in m2
- Determine the value of the magnetizing force (H). To determine the magnetizing force (H), we use the formula H = B/µ0µr, where B is the flux density in Weber/m2—the value of µ0 absolute permeability is 4πx10-7. The value of µr relative permeability of the material, if given, we can use it to calculate H. However, if the value of µr is not given, we can determine it from the B-H curve using the value of H.
- The magnetizing force(H) is obtained by multiplying the magnetizing force of each section, H1, H2, H3, and Hg, with their respective sections, l1, l2, l3, and lg.
- To find the total MMF of a series magnetic circuit, add the Hx l values of each section. The total MMF is.
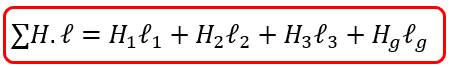
Conclusion:
It is essential for engineers and designers working on electromagnetic devices to understand series magnetic circuits. These circuits are crucial in optimizing the performance of magnetic components such as transformers or inductors. By considering the arrangement and properties of magnetic materials, engineers can design efficient and reliable systems that effectively harness the power of magnetic fields in various applications.