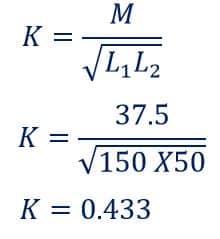The Coefficient of coupling shows the fraction of magnetic flux produced by the current in one coil that links with the other coil.
When coil A receives voltage, current flow through it and generates flux(Φ). The generated flux links to coil B. However, it is not possible that the whole flux links to coil B.
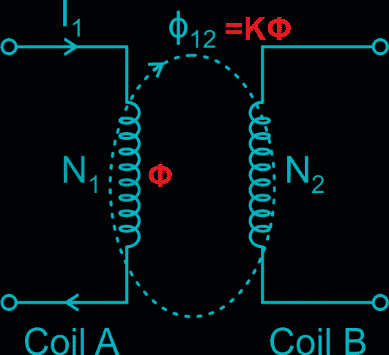
Some part of the flux leaks through the path and because of this leakage flux coil B receives less flux. Thus, the fraction of flux linking to coil B is called the coefficient of coupling(K). Its value is between 0 and 1. If K=0, the flux produced in coil A does not link at all to coil B. If K=1, the entire flux produced by coil A links to coil B.
Formula Derivation
When current I1 flow in coil A, the self-inductance and mutual inductance of the coil are;
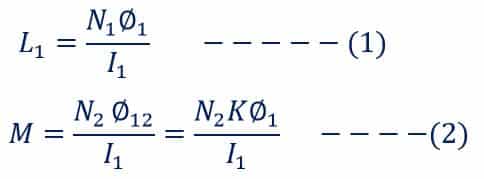
When current I2 flow in coil B, the self-inductance and mutual inductance of the coil are;
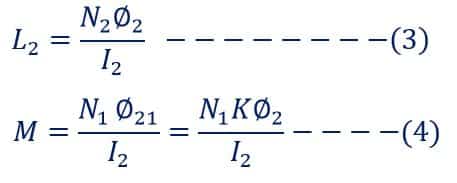
Multiplying equations(2) and(4), we get;
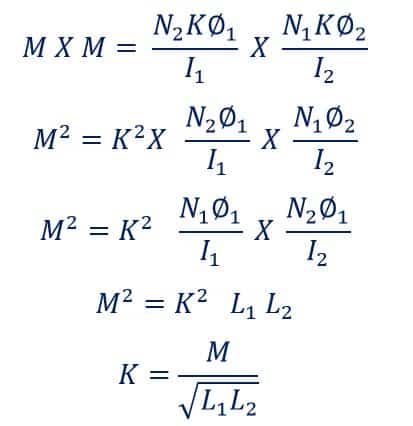
Note: The value of the Coefficient of coupling is always less than one and its maximum value is one. If the value coefficient of coupling is equal to one, then it is said to be a perfect coupling. In this condition, the entire flux generated in one coil fully links to another neighboring coil.
Relationship between Mutual inductance and Coefficient of Coupling
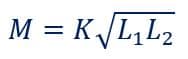
If the coils have perfect mutual coupling, then k=1
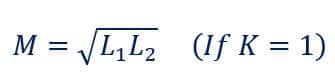
Solved Problem on Coefficient of Coupling
Two coils connected in a series-aiding manner have a total inductance of 275 mH. When connected in a series-opposing configuration, the coils have a total inductance of 125 mH. If the inductance of one coil (L1) is three times the other, find L1, L2, and M. What is the coupling coefficient?
L1 +L2 + 2M = 275 ——(1)
L1 +L2 – 2M =125 ——(2)
Adding(1) and(2)
2L1 +2L2 =400
L1 +L2 =200—–(3)
L1= 3 L2—–(4)
Putting value of (4) in (3)
L1 +L2 =200
3L2 +L2 =200
L2 =50 mH
L1 =150 mH
L1 +L2 + 2M = 275
150+50+2M =275
M= 37.5 mH