Transient Response of Capacitor- RC Circuit Transient Behavior

Transient response of capacitor shows the current and voltage response in an RC circuit after a change in the applied voltage to the circuit.

A capacitor is one of the fundamental passive circuit elements. It is used in an electrical or electronic circuit to store electrical energy in the form of electrostatic charge. Therefore, a capacitor can be considered a secondary small cell. The important characteristic of a capacitor is its transient response or behavior. This is because, a capacitor when connected to a source of electrical energy like a battery, starts storing charge, and once it is fully charged, it stops the flow of current in the circuit.

Therefore, it is important to study the behavior of a capacitor during its charging and discharging conditions, generally termed the transient behavior of the capacitor. In this article, we will study and understand the transient response of a capacitor during its charging and discharging period. Let’s start with the basic definition of the transient behavior of the capacitor.

The electrical behavior of a capacitor that does not have a constant voltage or current, also the variation in the current and voltage is not periodic and controlled, is referred to as the transient response or behavior of the capacitor.

The transient behavior of a capacitor is generally seen during the charging and discharging period of the capacitor.

Now, let us study the transient behavior of the capacitor during charging and discharging individually.

Transient Response of Capacitor During Charging

The electrical circuit arrangement for charging a capacitor is shown in the following figure.

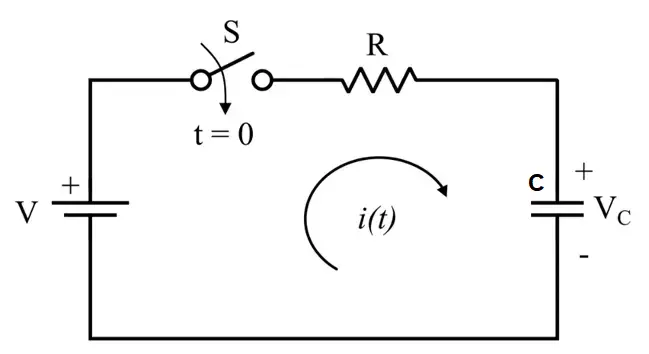
In this circuit, the capacitor of capacitance C is being charged to a voltage V through a resistor R.

When the switch S is closed, a current will start flowing in the circuit suddenly, let this current at a time instant t is i(t).

Capacitor Charging Equation

If V_C(t) is the voltage developed across the capacitor at the considered time instant t. Then, according to KVL, we can write the mesh equation as follows,

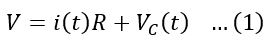
And the current i(t) flowing in the circuit at time t is given by,

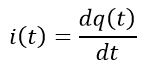
q (t) is the charge accumulated at the capacitor at time t.

Then, the total charge stored in the capacitor is,

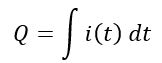
Also, for a capacitor, the charge stored is given by,

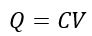
Therefore, the total charge stored in the capacitor will be

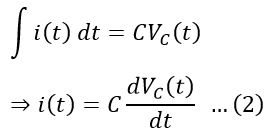
From equations (1) and (2), we get,

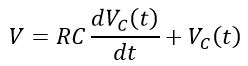
Rearranging this equation, we get,

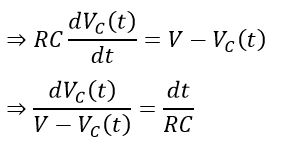
Integrating on both sides with respect to time, we get, transient response of capacitor equation as;

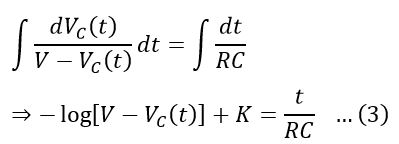
Here, K is an integration constant whose value can be determined from the initial conditions of the capacitor, i.e.

Let at the time of switching, t = 0, and V_C(t) = 0, then, the equation (3) can be written as

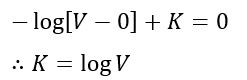
Substituting the value of K in equation (3), we have,

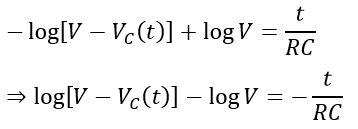
As per the rule of logarithmic, we have,

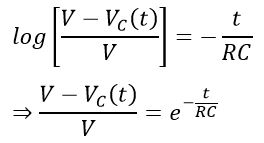
Therefore,

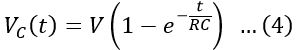
This is the transient equation of the capacitor during charging. It shows that voltage across a capacitor during the charging period increases exponentially.

For a capacitor, the term RC is referred to as its time constant. It is defined as the time required by the capacitor to develop a voltage equal to 63.2% of the supply voltage.

The voltage across the capacitor, when t = RC,

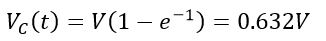
Now, let us discuss the transient response of the capacitor during discharging period.

Transient Response of Capacitor During Discharging

Let us consider a fully charged capacitor C and the voltage across the capacitor is equal to V. When the capacitor is connected across a load resistor R as shown in the following figure, it will start losing its charge, i.e. discharging. After some time, the capacitor will be fully discharged.

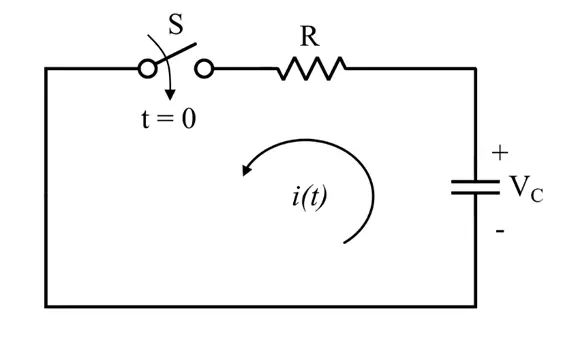
Now, let us use the discharging equation of the capacitor to understand capacitors’ transient response during discharging period.

Capacitor Discharging Equation

Applying KVL in the loop, we get,

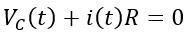
From equation (2), putting the value of i(t), we get,

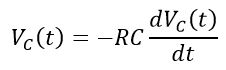
Rearranging the equation, we get,

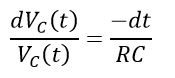
Integrating on both sides with respect to time, we get,

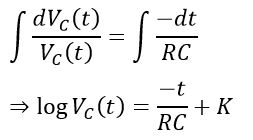
Here, K is a constant whose value can be determined from initial conditions, i.e.

At t = 0; V_C(t) = V, therefore,

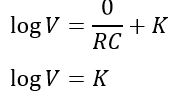
Therefore,

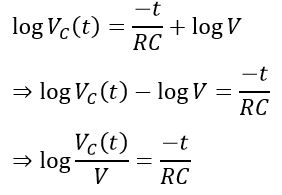
Taking antilog on both sides, we have,

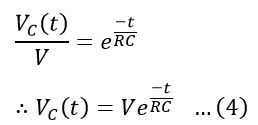
Now if we put RC = t in the above equation, we get.

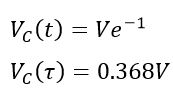
This is discharging equation of the capacitor. The transient response of the capacitor during discharging indicates that during discharging period the capacitor shows exponentially dying transients.

Hence, this is all about the transient response of a capacitor during its charging and discharging period.

• Capacitor Charge & Time Constant Calculator
• Power Quality Terms and Definitions
• Breaking Current Capacity Of circuit Breaker
• Types of Voltage Surge
• Response Time Test of RTD & Thermocouple