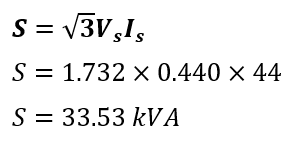The maximum current a transformer can deliver to loads at the rated voltage is known as a transformer rating. It is expressed in VA, kVA, or MVA (volt-amperes). You can find this data on the transformer’s nameplate.
What is the Rating of Transformer?
The transformer steps up and steps down the voltage as per the user’s requirements. The transformer can deliver the current to load as per the transformer’s full load secondary current. The maximum secondary current that a transformer can deliver at the specified voltage decides the VA of the transformer. Therefore, a transformer must not be operated above its full load capacity to avoid excessive temperature rise. The losses cause the de-rating.
The excessive temperature rise affects the full load current delivering capacity of the transformer. The no-load losses increase with an increase in the frequency and or voltage, and the copper loss increases if the load power factor is more lagging, which demands more current from the transformer, and the copper loss increases. The losses can be kept within the limit by maintaining the rated voltage, frequency, and load current.
The losses cause a temperature rise in the transformer, and if a transformer is operated above its specified temperature limit, the winding insulation is apt to fail. The temperature can be held within the safe limit by proper transformer cooling.
The losses depend on the V and I—the current I depends on the type of load and its rating. If the load is inductive or capacitive, then the power factor of the load should be considered for calculating the transformer rating. The load with a lagging power factor demands more current to meet its active and reactive power requirements. Therefore, the increased current causes more loss in the transformer and affects the transformer’s current-delivering capacity.
The transformer rating depends on the voltage(V) and current(I). The product of voltage and current is the apparent power or VA rating, and it is called the transformer rating. The designer considers the maximum VA of the transformer while designing. The transformer is specified for apparent power or– VA.
The transformer’s primary VA is equal to the secondary VA plus the losses in the transformer. If the losses increase, the secondary VA delivery will be affected because of the rise in the temperature of the transformer. Generally, the losses of the transformer are negligible. The primary VA is equal to the secondary VA.
The VA rating marked on the nameplate is applicable for both the winding and the VA of the primary and secondary winding of the transformer is the same. For a 440/220 Volts, 100 KVA transformer, the primary winding VA is 100 kVA, and the secondary winding kVA is also 100 kVA.
Formula for Transformer Rating
Single-phase Transformer

The formula for ratings in kVA is,

Three-phase Transformer

The formula for ratings in kVA for 3-phase transformer is,

Solved Problems of Transformer Rating
Let’s understand the concept of transformer rating with examples.
Problem-1:
A single-phase transformer delivers 60 amperes of current to a load at 440 volts. What is the transformer’s rating?
Given Data-
Voltage(V) = 440 V
Current(I) = 60 A
The transformer rating is;
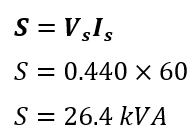
Problem-2:
A three-phase transformer’s secondary voltage is 440 volts, supplying current to a resistive load of 10 ohms. Calculate the transformer rating.
The secondary current is;
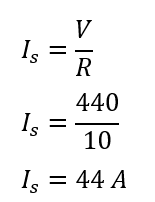
Transformer Rating