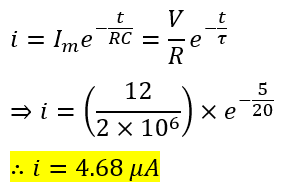This article describes the RC charging circuit and RC network time constant. A capacitor does not instantly charge, and the voltage across the capacitor builds slowly according to the RC time constant.
What is a Capacitor?
A capacitor is a passive circuit element used in electrical and electronic circuits to introduce capacitance. The capacitance is a capacitor’s property by which it can hold electrostatic charge.
The capacitance of a capacitor is given by,
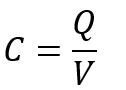
Where Q is the charge stored in the capacitor, and V is the applied voltage.
Hence, the capacitance can be defined as the charge per unit volt.
To charge a capacitor, we have to apply a voltage across it. This applied voltage polarizes the dielectric medium between the capacitor and creates an electric field inside the capacitor. Under this state, the capacitor is said to be charged.
However, it is important to understand the charging process of a capacitor, as it plays a vital role in circuit analysis.
RC Charging Circuit
To analyze the behavior of a capacitor during charging, consider the following RC circuit, which is called RC charging circuit.
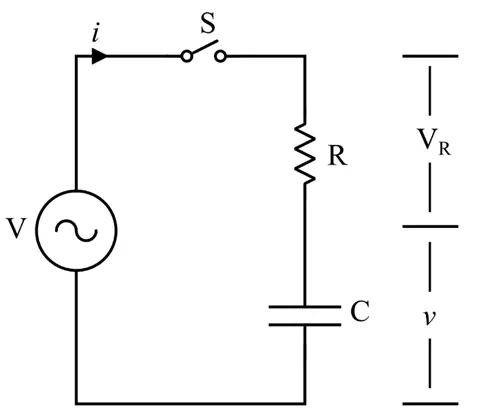
It consists of a fully uncharged capacitor and a resistor connected in series. This series combination of R and C is connected to a source of voltage V through a switch S.
Initially, the switch is opened, and the capacitor is fully uncharged. When the switch is closed, an electric current will start flowing through the circuit due to the applied voltage.
Since the capacitor is uncharged, the charging current will be maximum at starting and decrease with the capacitor’s charging.
The circuit current will become zero once the capacitor is fully charged to the applied voltage.
Now, let us perform a mathematical analysis of the circuit to derive the expression of the RC charging current.
Expression of RC Charging Current
Consider the instant when the switch is closed. At this instant, the capacitor is fully uncharged. Hence, the voltage applied will force a maximum current to flow through the circuit. Since there is no voltage across the capacitor, the total applied voltage will drop across the resistance R, i.e.,
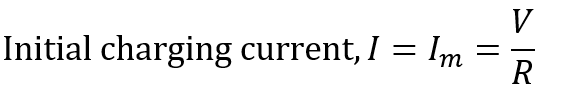
Now, consider any instant during charging. When the capacitor starts charging, the voltage across it increases, and the circuit current will decrease, i.e.,
Let at time instant ‘t’,

At this instant, the applied voltage will be the sum of the voltage drop across the resistor and voltage across the capacitor, i.e.,
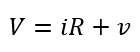
Since the current through a capacitor is given by,
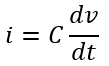
Therefore,
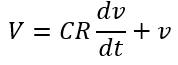
Rearranging the equation, we get,
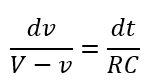
Integrating on both sides, we have,
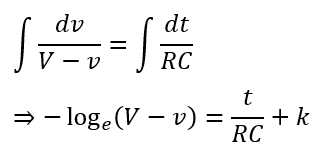
Here, k is a constant whose values are determined from the initial conditions of the circuit, i.e.,
At initial conditions, t = 0, and v = 0, thus,
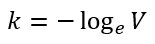
Substituting in the above expression, we get,
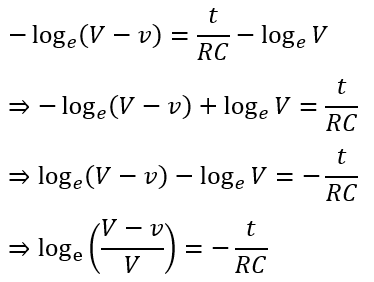
Taking antilog, we get,
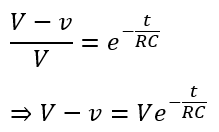
On rearranging this equation, we get,
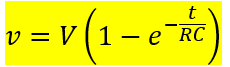
This is called the charging equation of the capacitor. From this RC charging circuit equation, it can be seen that the voltage across the capacitor during charging increases exponentially.
Now, let us derive the expression of the charging current of the capacitor.
For a capacitor,
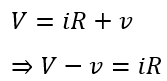
Also,
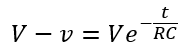
Comparing these two equations, we get,
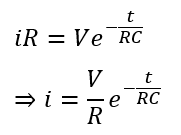
Since Im= V/R, thus,
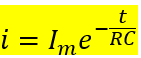
As it can be seen, the charging current of a capacitor decreases exponentially.
Now, let us discuss the time constant of the RC charging circuit.
Time Constant of RC Circuit
The time constant of an RC circuit is defined as the time required to charge the capacitor to its final steady value of voltage.
In other words, the time constant of an RC circuit is the time required to reach the voltage across the capacitor equal to 0.632 times its full voltage.
Mathematically, the time constant of an RC circuit is given by the product of resistance and capacitance, i.e.
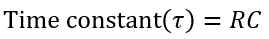
Hence, this is all about the RC charging circuit and the time constant of the RC circuit. Let us now consider an example to understand the application of formulae in solving problems.
Solved Problem on Capacitor Charging & Time Constant
Numerical Example – A capacitor of 10 µF is connected to a source of 12 V supply through a resistance of 2 MΩ. Calculate the value of charging voltage and current at t = 5 seconds. Also, calculate the time constant of the circuit.
Solution – Given,
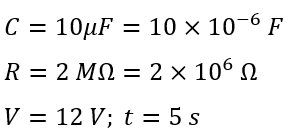
The time constant of the circuit is
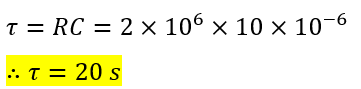
The charging voltage at t = 5 s will be,
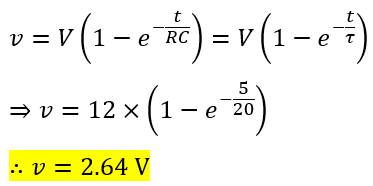
The charging current is