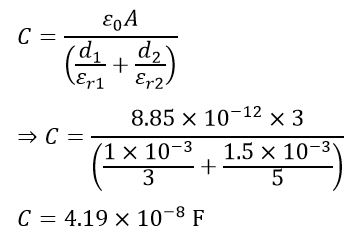A parallel plate capacitor has two conductive plates in parallel separated by some distance. It has a dielectric medium between the plates and stores energy in the form of an electric field.
A capacitor is one of the basic electronic circuit elements used in a variety of electrical and electronic circuits. A capacitor is nothing but a device that can store electrical energy in the form of an electric field. Based on the construction, there are several different types of capacitors.
What is a Parallel Plate Capacitor?
A parallel plate capacitor is constructed by placing two metal plates parallel to each other and separated by an insulating medium.
It is the simplest type of capacitor. The typical construction of it is shown in the following figure.
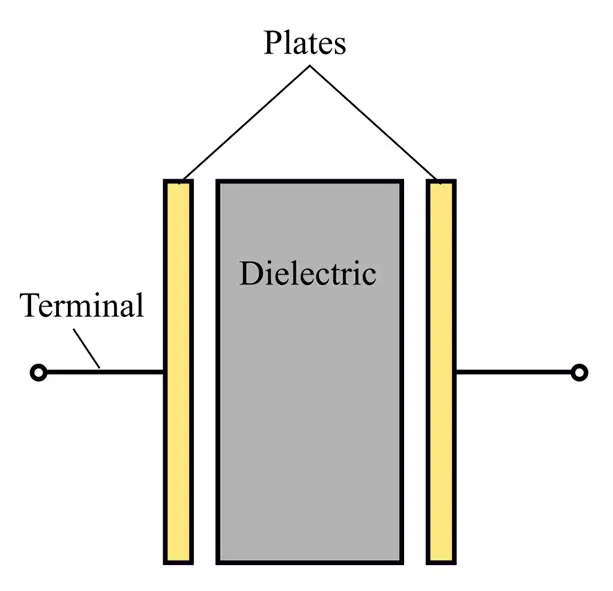
It has two metal plates and an insulating medium between the plates. The insulating medium is a dielectric material that can store electrical energy in the form of an electrostatic field. Some commonly used types of dielectric materials are air, mica, wax paper, etc.
Types of Parallel Plate Capacitors
Parallel plate capacitors can be classified based on the dielectric medium used. The following are some common types of parallel plate capacitors.
- Air Capacitor – In this type of capacitor, air or vacuum is used as the dielectric medium between the plates of the capacitor to store electrostatic charge.
- Mica Capacitor – In this type of capacitor, mica is used as the dielectric medium. The use of mica as a dielectric medium increases its capacitance.
- Ceramic Capacitor – It has ceramic as the dielectric medium to store electric charge.
- Paper Capacitor – It has wax paper as the dielectric medium between the metal plates of the capacitor.
Parallel Plate Capacitor Formula
The capacitance of a parallel plate capacitor is;
- directly proportional to the area (A) of each plate.
- inversely proportional to distance (d) between the plates.
- directly proportional to the permittivity of the dielectric medium.
Therefore,
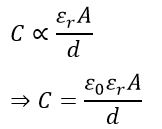
Where ε0 is the dielectric constant of air, εr is the dielectric constant of the medium between the plates.
For an air capacitor, εr = 1, therefore, the capacitance of an air capacitor is given by,
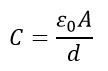
Construction of Parallel Plate Capacitor
A parallel plate capacitor is simply constructed by separating two parallel metal plates by a dielectric medium. However, there can be the following two types of parallel plate capacitor constructions namely,
- Capacitor with Uniform Dielectric Medium
- Capacitor with Composite Dielectric Medium
Let us now discuss each construction in detail along with their capacitance computation.
(1). Parallel Plate Capacitor with Uniform Dielectric Medium
A capacitor with a uniform dielectric medium is shown in the following figure.
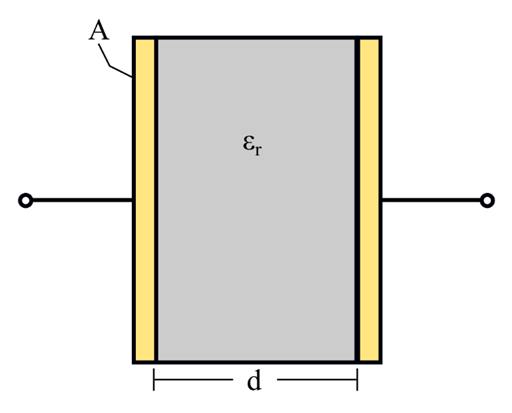
It consists of two metal plates, each of surface area A, and these plates are separated by a uniform dielectric medium of thickness d. If the relative permittivity of the dielectric medium is εr, then the capacitance of the capacitor is given by,
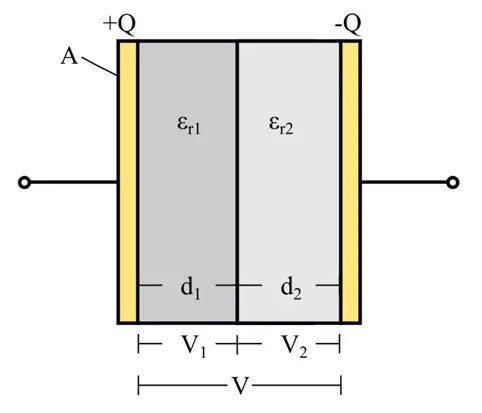
(2). Parallel Plate Capacitor with Composite Dielectric Medium
In this type of construction, different dielectric mediums are placed between the plates of the capacitor. The following figure shows a parallel plate capacitor with two dielectric mediums with two different relative permittivities, i.e. εr1 and εr2 respectively.
Parallel Plate Capacitor Formula Derivation
For this type of capacitor, we can derive the capacitance formula as follows:
The electric field intensity in the two dielectric fields is given by,
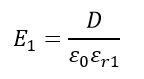
And,
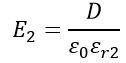
Where D is the charge density and is given by,
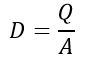
It is the same for both dielectric mediums as the total charge per plate is the same, i.e. Q coulombs.
If the total voltage across the capacitor is V and the voltages across two dielectric regions are V1 and V2 respectively, then
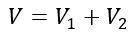
Since, V = E × d, therefore
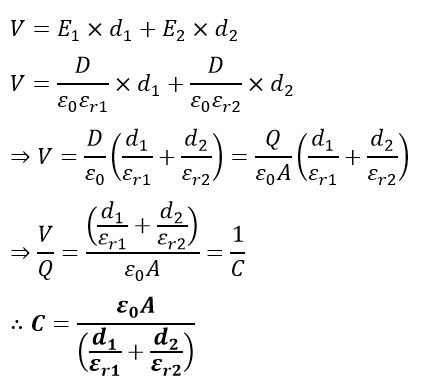
For a capacitor with n-composite dielectric mediums, we get,
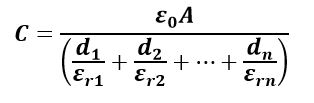
Advantages of Parallel Plate Capacitors
The following are some major advantages of a parallel plate capacitor over other types of capacitors:
- Easy to design and manufacture.
- Compact in size, making them versatile.
- Have very low inductance because of the compact design
- Provide faster response time
- Very low internal resistance, making them energy efficient.
Disadvantages
The following are some key disadvantages.
- For the same capacitance values, these capacitors have larger sizes and higher weights as compared to other types of capacitors.
- Due to expensive dielectric materials, these capacitors are more expensive.
- Extreme environmental conditions like high temperature, humidity, etc. can greatly influence the operation and performance of the capacitors.
- They have limited voltage ratings and frequency responses.
- They have a capacitance tolerance range.
Applications
Parallel plate capacitors are widely used in the following applications:
- Used in various electronic devices like, filters, UPS, oscillators, etc.
- Applications in power electronic circuits like inverters, choppers, motor drives, etc.
- Used in various communication devices like radio transmitters, receivers, wireless antennas, etc.
- Used for smoothening the voltage fluctuations in power supplies.
- They are used in tuning circuits to adjust resonance frequency.
- Also used in various sensors like position sensors, pressure sensors, proximity sensors, etc.
- They provide protection against electrostatic discharge (ESD).
Numerical Examples
Numerical Example (1)
Calculate the capacitance of a parallel plate capacitor having two plates of area 20 m2 and separated by a dielectric of 3 mm thick and of relative permittivity 4.
Solution – Given data,
Area of plates, A = 20 m2
Distance between the plates
d = 3 mm = 3 × 10-3 m
The Relative permittivity of the dielectric
εr = 4
The capacitance of the given capacitor will be,
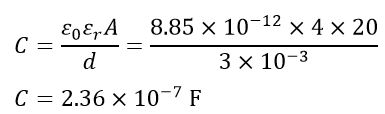
Numerical Example (2)
A parallel plate capacitor has two metal plates of area 3 m2 and spacing by two layers of different dielectric mediums. The relative permittivity of these layers are 3 and 5 respectively and thickness are 1 mm and 1.5 mm. Calculate the capacitance of the capacitor.
Solution – Give data,
Area of plates, A = 3 m2
Thicknesses of dielectrics,
d1 = 1 mm
= 1 × 10-3 m;
d2 = 1.5 mm
= 1.5 × 10-3 m
Relative permittivity,
εr1 = 3 and
εr2 = 5
The capacitance of the capacitor will be,