In this article, we will discuss load equalization in electrical drives and the method of load equalization. So, let’s begin with the basic definition of load equalization.
What is Load Equalization?
In electrical drives, the process of smoothing the load fluctuation is called load equalization. Load equalization is necessary because an electrical drive having a fluctuating load draws unbalanced currents from the supply. This current is very high during the peak interval. Also, the fluctuating load causes a large voltage drop in the supply system, which may damage the system equipment.
In the load equalization process, the energy is stored in the system during the light load period, which is then used during the interval of peak load. Consequently, the electrical energy demanded from the source remains constant throughout the operation.
Load fluctuation is very common in some electric drives, like pressing machines. In a pressing machine, load fluctuation occurs because a large torque is required for a short duration, and for the rest of the time, the torque required is zero. Other examples of electrical drives having load fluctuation are electric hammers, reciprocating pumps, rolling mills, etc.
Method of Load Equalization in Electrical Drives
In electrical drives, load equalization is achieved with the help of a flywheel. A flywheel is a wheel of heavyweight. This flywheel is attached to the shaft of the electric drive, and it acts as a reservoir of energy.

During the period of light loads, the flywheel stores extra energy received from the supply. During periods of heavy loads, the speed of the electrical drive decreases. Under this condition, the flywheel redistributes the stored energy to meet the load demand. Hence, the electric power drawn from the supply remains constant throughout the operation of the drive.
Flywheel Calculation:
For load equalization, we have to calculate the moment of inertia of the flywheel. The calculation is explained below.
Let us consider a flywheel mounted on the shaft of the electrical drive for load equalization. If the drive has the linear speed torque characteristics expressed by the following equation,
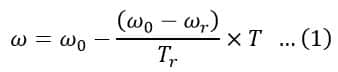
Where ω is the instantaneous speed, ω0 is the no-load speed, ωr is the rated speed, T is the instantaneous torque, and Tr is the rated torque.
Because of the slow response due to large inertia, the drive motor can be assumed to be in electrical equilibrium during the transient operation of the drive system. In that case, equation (1) also applies to transient operation.
Differentiating the equation (1) with respect to t and multiplying both sides by J (moment of inertia), we get,
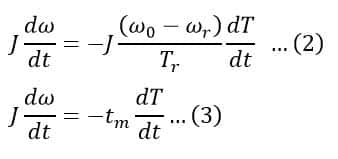
Where,
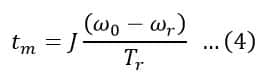
Here, tm is the mechanical time constant of the drive motor. It is defined as the time required for the motor speed to change by ω0 to ωr when the torque remains constant at the rated value Tr.
From equations (2) and (3), we get,
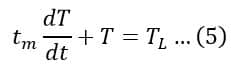
Equation (2) shows that at any instant, a portion of the torque demanded by the load is met by the developed torque of the motor, whereas the flywheel contributes the rest portion.
The instantaneous value of torque developed by the motor during either a heavy or a light load period can be obtained by solving equation (2). It will be of the form given below,
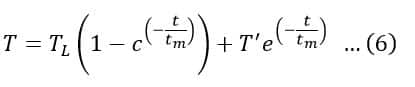
Where T’ is the torque developed by the motor at the instant of application or removal of the load. By using equation (6), the torque developed by the drive motor at the end of the heavy load is given by,
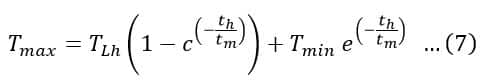
Where Tmin is the motor torque at the end of the light load. It is given by,
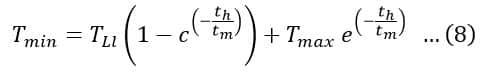
From equations (7) and (8), we get,
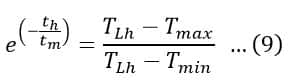
And,
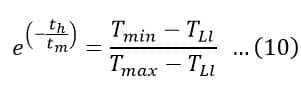
Also, from equation (4), we have,
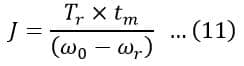
Using equations (9) and (10), we get,
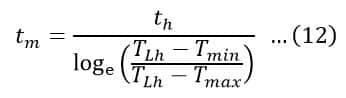
Or,
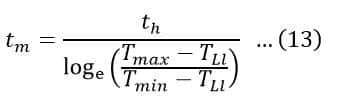
Therefore, the moment of inertia of the flywheel is given by,
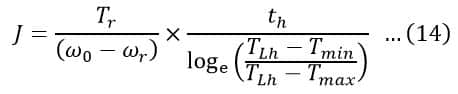
Or,
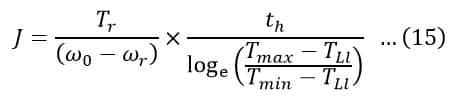
Thus, the moment of inertia of the flywheel can be calculated either from equation (14) or (15).
Further, the moment of inertia can also be calculated by using the following expression,
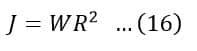
Where, W is the weight of the flywheel in kg, and R is the radius of the flywheel in meters.
Hence, this is all about load equalization in electrical drives and the method of load equalization.