This article describes the Decibels formula, its calculation, and its applications. Decibels are a unit of measurement used to express the relative intensity or power of a signal, especially regarding sound, electronic circuits, or telecommunication devices. It is indicated by ‘dB’.
The decibel (dB) uses a logarithmic scale to draw a comparison between two quantities like Power, Voltage, current, or intensity. This unit is commonly used in the fields of signal processing, audio engineering, telecommunications, and electronics.
The main advantage of using deciBels is that it uses the base ten logarithms, which are commonly used in mathematics. Thus, a logarithmic scale helps compare quantities that may have a big ratio.
The term ‘deciBel’ is made up of two terms – ‘deci’ and ‘Bel,’ which means – ‘one-tenth of a Bel.’ The unit ‘Bel,’ however, is not commonly used now. Bel is a unit named after Alexander Graham Bell.

Formula to calculate Decibels
The formula to calculate deciBels depends on what you are measuring. Here are some formulas to calculate deciBels for a given quantity.
DeciBels Formula for Power (dBm):
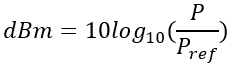
Where P is the power being measured, and Pref is the reference power with respect to which measurement is being taken (usually 1mW).
DeciBels for Voltage (dBV):
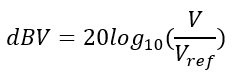
V is the voltage being measured, and Vref is the reference voltage for which the measurement is being taken (usually 1V).
DeciBels for Current(dBA):
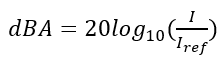
Where I is the current being measured, and Iref is the reference current with respect to which measurement is being taken (usually 1A).
DeciBels Formulas for Comparison of Two Electrical Quantities:
While comparing any two values, let’s say V1 and V2, the formula that is usually applied to calculate deciBels is given as
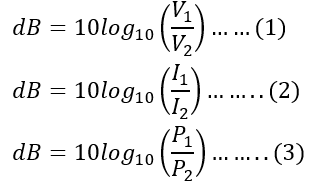
For example, if a system has a power output of 10mW, then it can be represented in decibels(dBm) with reference to 1mW as
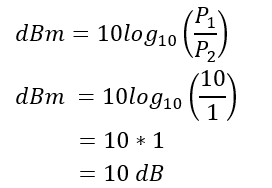
deciBels(dB) are logarithmic in nature. The logarithmic nature of deciBels causes a small change in dB to represent a significant change in the actual value. For example, a 3dB increase in power represents a doubling of power, while a 10dB increase represents a tenfold increase.
Why logarithmic scale and not linear scale?
There are several advantages of the use of a logarithmic scale instead of a linear scale in applications where we calculate and represent intensity in decibels. Quantities like sound intensity, electrical power, and signal strength can vary over an incredible range of values.
For example, the intensity of sound a human can hear. It can range from the faintest to the loudest noise a human can hear. The range is so wide that representing this intensity on a linear scale is practically a tough task. A logarithmic scale can represent this easily in a small range and in a compact way.
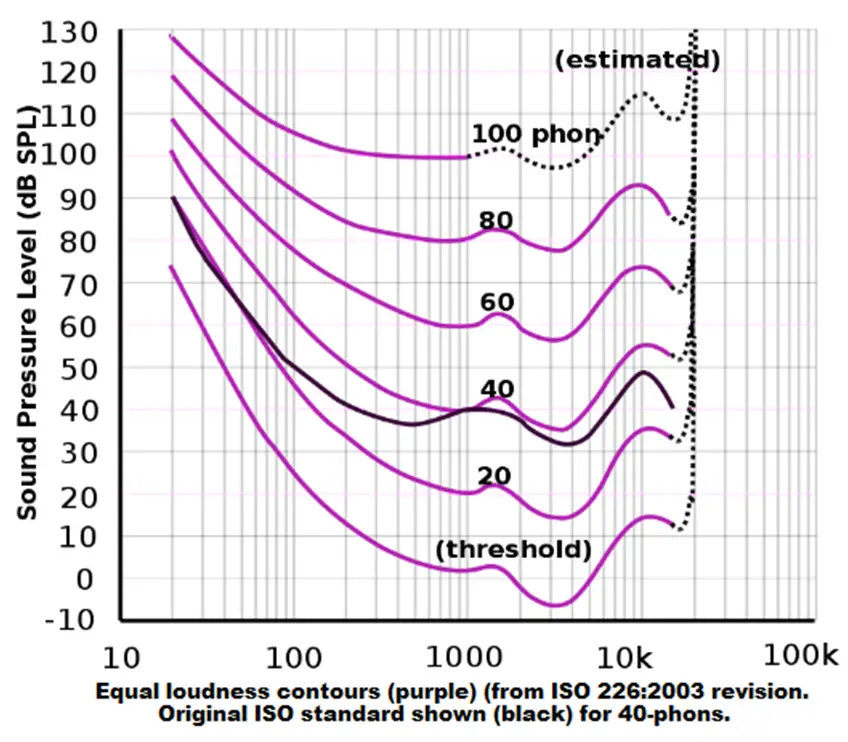
Other than this, a logarithmic scale matches our perception of physical quantities like the intensity of light and sound, which is inherently logarithmic. A linear scale will not be able to quantify these perceptions accurately.
The logarithmic scale used for dB calculation also helps in relative comparison between two values. This is helpful in applications like telecommunications, where we calculate sound-to-noise ratio (SNR) to improve signal quality.
These are some of the advantages of using a logarithmic scale for decibel calculation in place of a linear scale.
Decibel abbreviations and their Meaning
dB is calculated in various applications, from audio and radio frequency to power, voltage, and current in an electronic system. In each of these quantities, deciBel refers to different meanings. Thus, there are different abbreviations used in different applications. Some of these abbreviations are:
| Abbreviations | Description |
| dBA | “A” weighted sound pressure or sound intensity measurement. |
| dBc | Gain of an antenna with reference to a half-wave dipole in free space |
| dBd | Level with reference to full-scale reading |
| dBFS | Gain of an antenna with reference to an isotropic source, i.e., one that radiates equally in all directions. |
| dBi | Power level with reference to 1 watt This is all about deciBels, its meaning, applications, and calculations |
| dBm | Power level with reference to 1 mW |
| dBV | Power level with reference to 1 watt This is all about deciBels, its meaning, applications, and calculations |
| dBµV | Level with reference to 1 microvolt |
| dBW | Power level with reference to 1 watt This is all about deciBels, its meaning, applications, and calculations. |
Applications of deciBel
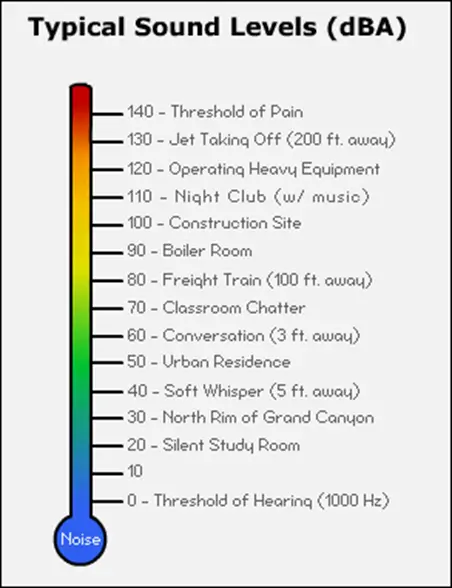
- Audio Engineering: Calculation of deciBels and its analysis is critical in the field of audio engineering for measuring and controlling sound levels. Sound levels are often measured in dB to represent the sound wave intensity mathematically. Legal restrictions and safe sound limits are prescribed in deciBels, and sound engineers are expected to ensure that their system adheres to these regulations. This helps set appropriate concert volumes, recording studios, home audio systems, etc.
- Telecommunications: In the field of Telecommunications, dB is used to measure the strength and quality of a given signal. The deciBel analysis of the signal helps in identifying and filtering out the unwanted noise. This causes an increase in the signal-to-noise ratio (SNR), indicating better signal quality for clear voice calls and reliable wireless and wired data transmission.
- Electrical and Electronics Engineering: In the field of Electrical and Electronics Engineering (EEE), decibel analysis is important to quantify voltage gain or attenuation in electronic circuits. Appropriate Amplifiers, filters, and attenuators are designed to ensure specific gains or losses in dB as required. The circuit is designed in a manner to provide the desired dB at the output.
- Radio Frequency (RF) Engineering: In systems like radio and microwave technologies, deciBels are calculated to measure the power of the signal and losses. Antenna gain, cable losses, and transmitter power are expressed in decibels (dB). Thus, the deciBel analysis helps in optimizing the performance of wireless communication systems like cellular networks and satellite communications.
- Astronomy and Astrophysics: Calculation of deciBels in astronomy and astrophysics is of utmost importance at many stages. In astronomy, for example, dB is used to analyze the relative brightness of heavenly bodies and celestial objects. The logarithmic decibel scale helps astronomers to describe the vast range of brightness in the universe more conveniently.
- Acoustics and Noise Control: It is important to assess and control noise levels in various places and environments per local laws and safety rules. These laws prescribe the safe and maximum permissible noise levels expressed in dB. These values are taken as a reference while designing audio systems like noise-canceling headphones to reduce unwanted noise and improve acoustic environments.
- Seismology: dB measurement is indispensable in the field of seismology as it is used to express the magnitude of an earthquake. Richter scale is used to measure the seismic energy release. It is a logarithmic scale and expresses the earthquake magnitude in decibels (dB). An increase by a whole number on the Richter scale means a tenfold increase in the amplitude and around 32 times more release of seismic energy.
These are some of the important applications of deciBel analysis in today’s world.