Coulomb’s Law in Vector Form – Formula, Derivation, Applications

Coulomb’s Law in vector form gives a complete and precise description of the electrostatic force acting between two charged particles. Unlike the scalar form, which only defines the magnitude of the force, the vector form includes both magnitude and direction, allowing a more accurate understanding of how charges interact in space.

This law states that the electrostatic force between two stationary point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. It also defines the direction of the force along the line joining the two charges — either attractive or repulsive depending on the nature of the charges.

In this article, we will explore Coulomb’s Law in vector form, its formula, history, derivation, and applications in detail.

What is Coulomb’s Law in Vector Form?

Coulomb’s Law in vector form defines the electrostatic force between two stationary point charges by taking both the magnitude and direction of the force into account. It extends the scalar form by representing the force as a vector quantity, which becomes crucial when dealing with systems involving multiple charges or three-dimensional charge arrangements.

In simple terms, it not only tells how strong the force is but also where it acts — i.e., along the line joining the two charges.

Key Characteristics of Coulomb’s Law in Vector Form

Proportional to the product of charges:
The force increases with the magnitude of the two interacting charges.

Inversely proportional to the square of the distance:
As the distance between charges increases, the force decreases rapidly with the square of the distance.
Directional dependence:
- Like charges repel each other.
- Unlike charges attract each other.
  The force acts along the line joining the centers of the two charges.

Medium dependence:
The force also depends on the nature of the medium separating the charges. A medium with higher permittivity reduces the force between charges.

Mathematical Formula of Coulomb’s Law in Vector Form

If two charges q₁ and q₂ are separated by a distance rrr in a medium with permittivity ε, the force on q₂ due to q₁ is given by:

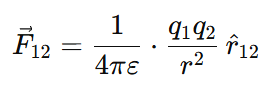
Mathematical expression of Coulomb’s Law in vector form showing the electrostatic force between two point charges q1 and q2 separated by a distance r in a medium with permittivity epsilon.

Where:

Explanation of terms in Coulomb’s Law vector form showing force F12, charges q1 and q2, distance r, permittivity epsilon, and unit vector r-hat12 indicating direction from q1 to q2.

This vector representation clearly shows both the magnitude and direction of the electrostatic force, making it a fundamental expression in electrostatics.

Coulomb’s Law Derivation in Vector Form

Consider two point charges q₁ and q₂ placed at points A and B with position vectors:

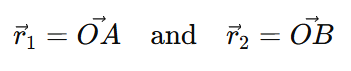
Where O is the origin.

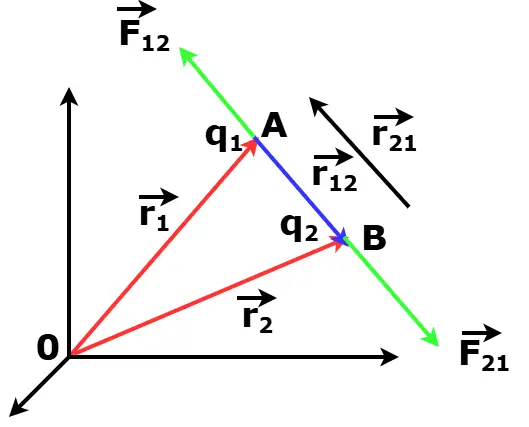
vector diagram for derivation of coulomb's law in vector form

1. Force on q₂ due to q₁

When q₁ exerts a force on q₂, the force vector F₁₂ acts along AB. Using the vector law of triangles:

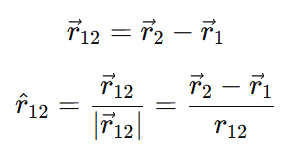
Diagram showing two charges q1 and q2 with force F12 along AB and position vectors r1 and r2, where r12 = r2 − r1 and r̂12 = r12 / |r12|.

The vector form of the force is:

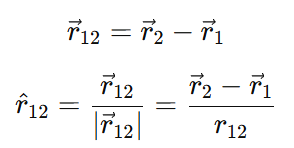
Vector form of Coulomb’s law showing force F12 = (1 / 4πε0) × (q1q2 / r12²) × r̂12, where r̂12 is the unit vector from charge q1 to q2.

Substitute r^{^}12:

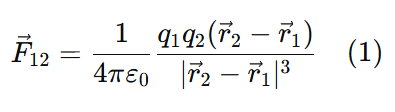
quation showing Coulomb’s law after substituting r̂12, where F12 = (1 / 4πε0) × (q1q2 (r2 − r1)) / |r2 − r1|³.

2. Force on q₁ due to q₂

When q₂ exerts a force on q₁, the force F21 acts along BA. Similarly:

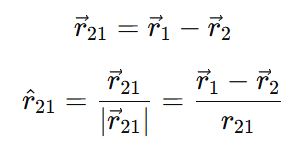
Diagram showing force F21 acting along BA when charge q2 exerts a force on q1, with position vectors r1 and r2, where r21 = r1 − r2 and r̂21 = r21 / |r21|.

The vector form of the force is:

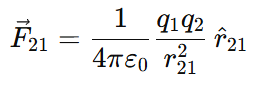
Vector form of Coulomb’s law for force on q1 due to q2, given by F21 = (1 / 4πε0) × (q1q2 / r21²) × r̂21.

Substitute r^{^}21:

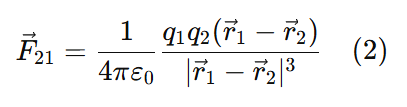
Equation showing Coulomb’s law after substituting r̂21, where F21 = (1 / 4πε0) × (q1q2 (r1 − r2)) / |r1 − r2|³.

Key Points:

F12=−F21 (Newton’s Third Law)
Denominator |r₂-r₁|^{^3} accounts for both magnitude and direction.
The force points away from the other charge if they are like charges, and toward it if they are unlike.

Applications of Coulomb’s Law in Vector Form

Coulomb’s Law in vector form is very useful in understanding how electric charges interact in real-life and theoretical situations. It helps engineers and students analyze both the magnitude and direction of electrostatic forces.

Analyzing complex charge systems:
It helps calculate the force between multiple charges placed at different positions.

Finding the net force on a charge:
The vector form allows easy determination of the total force on a charge due to several other nearby charges.
Electric field simulation:
Used in software like MATLAB, COMSOL, and ANSYS to model and visualize electric fields and potential distributions.
Electrostatic equilibrium study:
Helps find the point where the net electrostatic force on a test charge becomes zero.

Designing electrostatic instruments:
The principle is applied in designing sensors, charge meters, and electric field measuring devices.
Atomic and molecular studies:
Explains the attraction and repulsion forces between charged particles such as electrons and protons.
High-voltage engineering:
Used to analyze charge distribution and field intensity around insulators and conductors to improve insulation safety.

Conclusion

Coulomb’s Law in vector form provides a complete and realistic understanding of electrostatic interactions. By expressing force as a vector, it accounts for both magnitude and direction, making it indispensable for analyzing charge systems, electric fields, and electrostatic equilibrium. This vector approach forms the foundation for advanced topics in electromagnetism, field theory, and electrical engineering applications.

Related Articles: