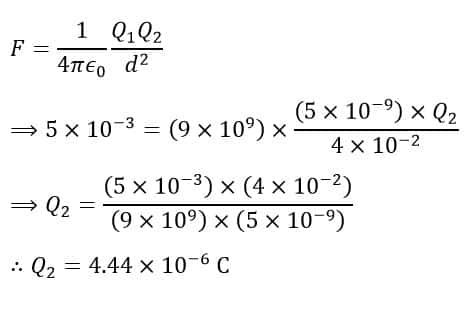In this article, we shall learn about Coulomb’s law in electrostatics. Here, we shall learn about the statement, formula, limitation, and applications of coulomb’s law.
In electrostatics, Coulomb’s law is the most fundamental concept which provides information about the electrostatic force acting between two or more charged bodies. The Coulomb’s was given by French physicist Charles Augustin de Coulomb in 1785. Coulomb’s law is also known as Coulomb’s inverse square law.
Statement of Coulomb’s Law
Coulomb’s law states that if there are two bodies placed in a medium (vacuum or dielectric), then the electrostatic force acting between the two bodies is directly proportional to the product of the charges on the bodies and is inversely proportional to the square of the distance between the charged-bodies.
Since Coulomb’s law gives the inverse square relationship between force and distance between two charged bodies. This is why the law is also known as Coulomb’s inverse square law.
Formula of Coulomb’s Law
Consider two charged bodies having charges Q1 and Q2 respectively, separated by a distance of d meters from each other as shown in the following figure.
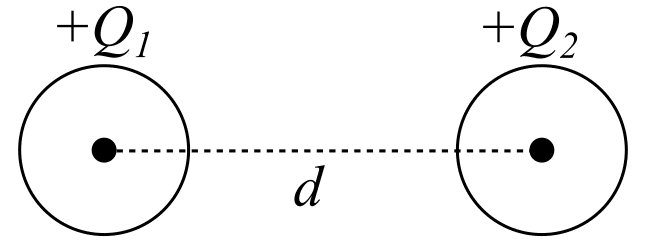
According to Coulomb’s law, we have,
- The electrostatic force acting between the two charge bodies is directly proportional to the product of charges on them, i.e.
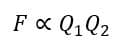
- The electrostatic force is inversely proportional to the square of the distance between the centers of the charged bodies, i.e.
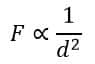
Hence, on combining these two equations, we get,
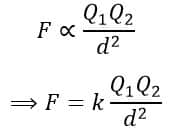
Where k is a constant of proportionality whose value depends on the medium in which the bodies are placed.
In the SI system, the value of k is given by,
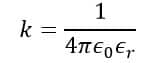
Where ε0 is the absolute permittivity of vacuum or free space and εr is the relative permittivity of the medium in which the bodies are placed.
The value of is ε0 equal to 8.85 × 10-12 C2/Nm2.
Therefore, the formula of the electrostatic force becomes,
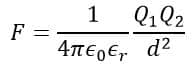
When bodies are separated from each other in a vacuum, then εr=1, thus,
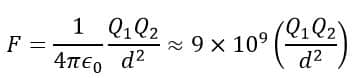
Note-
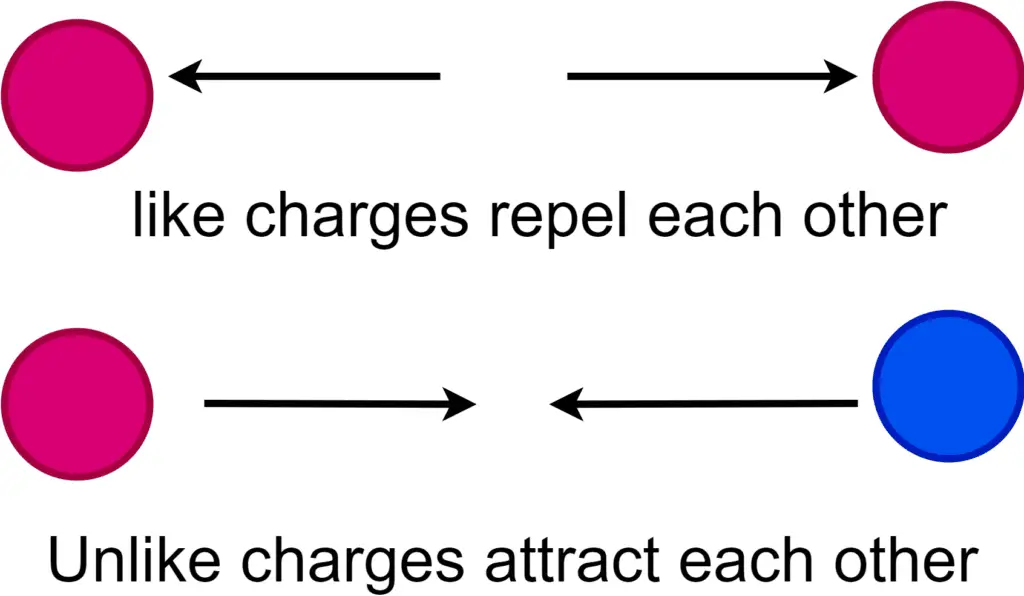
- If the charges Q1 and Q2 are like charges, i.e. both are of the same polarity (either positive-positive or negative-negative), then the force F acting between them is repulsive.
- If the charges Q1 and Q2 are unlike charges, i.e. both are of opposite polarity (positive-negative or vice-versa), then the force F acting between them is attractive.
Limitations of Coulomb’s Law
The following are the three major limitations where Coulomb’s law cannot be applied:
- Coulomb’s law is applicable only when the point charges are at rest.
- Coulomb’s law may not be applicable when the shape of charged bodies is arbitrary. It is because, for a body of arbitrary shape, we cannot determine the distance between the centers of bodies.
- We cannot calculate the force between the charges on the big planets using Coulomb’s law.
Applications of Coulomb’s Law
Coulomb’s law is the most fundamental law of electrostatic physics, the following are some major applications where coulomb’s law is used for calculations:
- Coulomb’s law calculates the electrostatic force acting between the point charges.
- Coulomb’s law also determines the distance between two point charged bodies.
- Coulomb’s law is also used to determine the electrostatic force acting on a point charge due to a number of charges.
Numerical Examples of Coulomb’s law
Numerical Example 1 – Calculate the electrostatic force between two charges 7 × 10-8 C and 2 × 10-7 C. These two charges are separated by a distance of 15 cm in free space.
Solution – Given data,
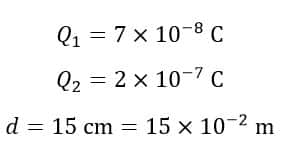
According to Coulomb’s law, we have,
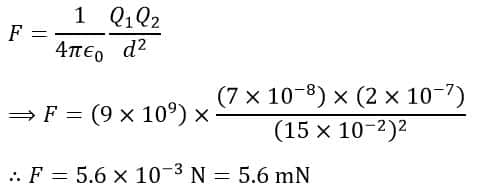
Numerical Example 2 – Two spheres are separated by a distance of 4 cm in air. The electrostatic charge on one sphere is 5 × 10-9 C and the electric force of attraction of 5 mN is acting between the spheres. Determine the electric charge on the second sphere.
Solution – Given data,
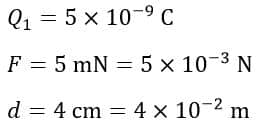
According to Coulomb’s law, we have,