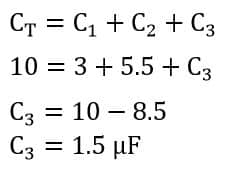
A capacitor is to be said to be connected in parallel if both of its terminals are connected to each terminal of another capacitor.
The voltage across each capacitor (VC) connected in the parallel is the same, and thus each capacitor has equal voltage and the capacitor voltage is equal to the supply voltage.
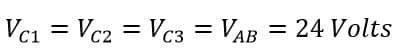
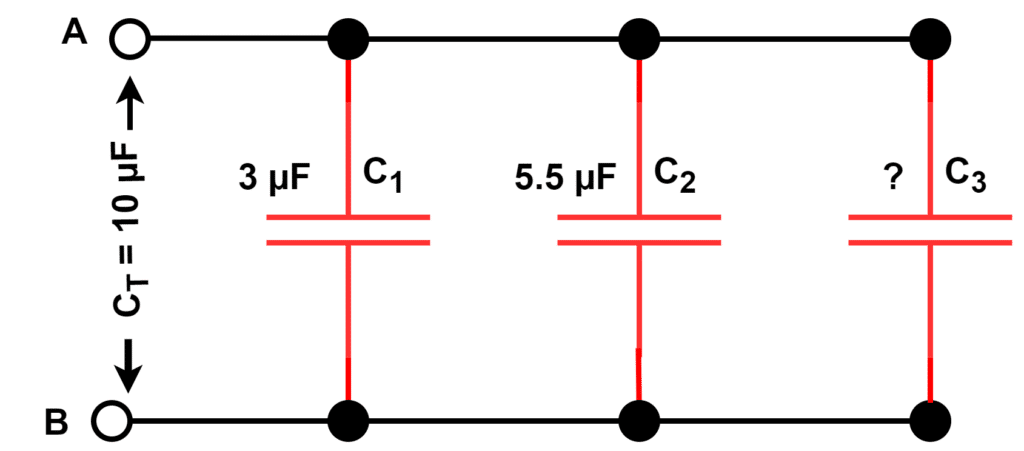
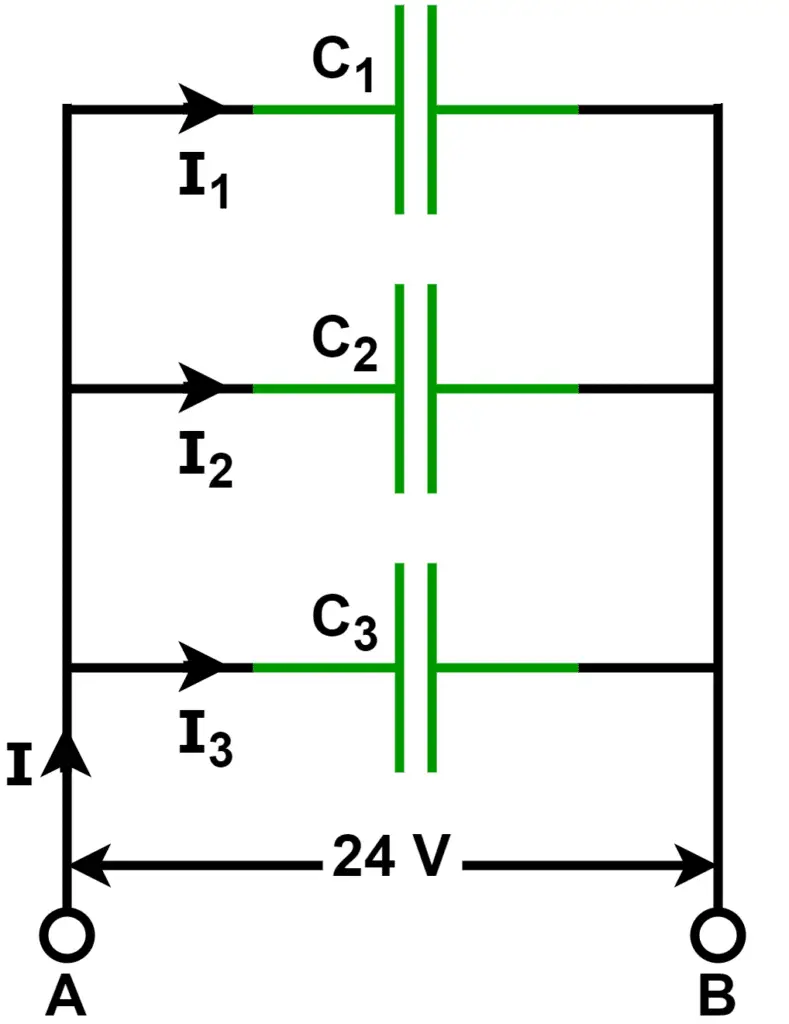
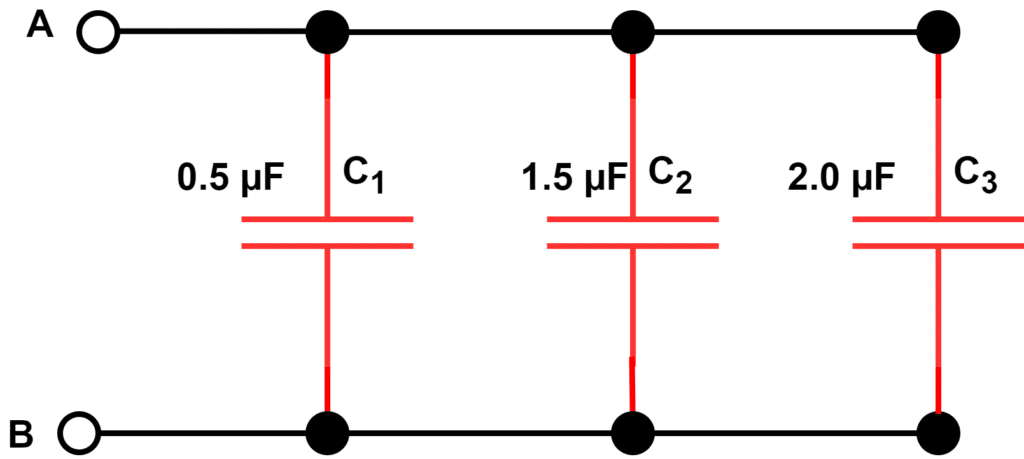
In the below-given figure, capacitors C1, C2, and C3 are connected in parallel between points A and B.
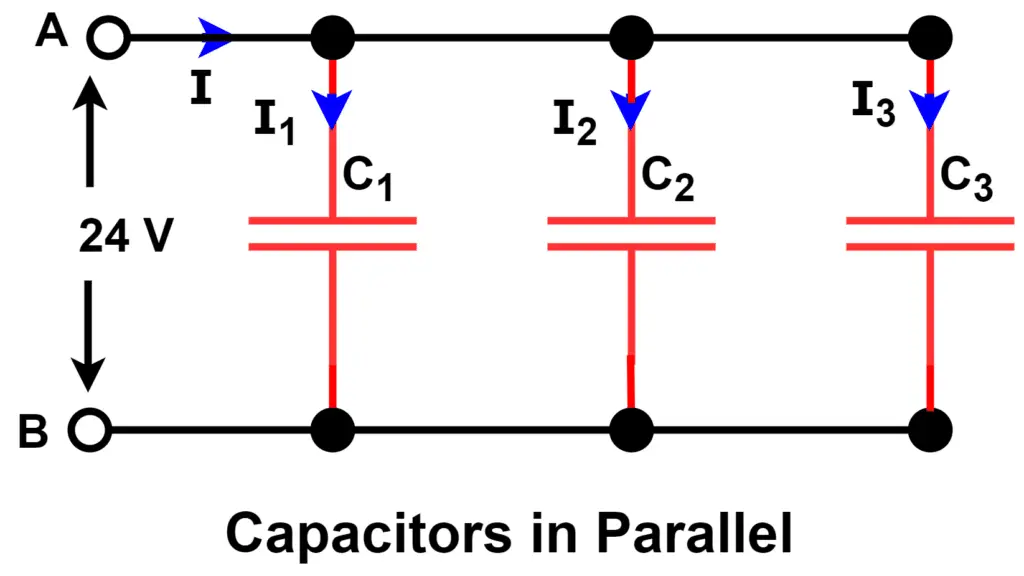
In the parallel combination of capacitors, each top plate of every capacitor is connected together. In a similar manner, the bottom plates of each capacitor is connected together. In the parallel connected capacitor, the total capacitance or equivalent capacitance CT is equal to the sum of all the individual capacitances.
The connection arrangement of the plates in this manner leads to increased overall plate area. We know, the capacitance increase with an increase in the plate’s surface area ( C = ε(A/d) ). Thus, the capacitance of the parallelly connected capacitor is always more than the individual capacitance of the capacitor.
If you recall the equivalent resistance of the series connected resistance, the resistance increases when the resistances are added in the series because the flow of electrons has to face more hindrance and causes resistance to increase. In a similar manner, the capacitors connected in parallel have more surface area because the individual capacitor plate area gets added to the other connected capacitors and thus we get more capacitance value.
Parallel Capacitors Equation
The current flowing through the capacitor depends on the capacitor’s capacitance and the rate of change of applied voltage.
The current through the capacitor C1 is;
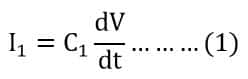
The current through the capacitor C2 is;
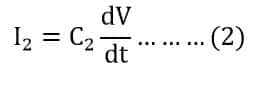
The current through the capacitor C3 is;
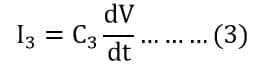
The total current of capacitors connected in parallel is equal to the sum of the currents in all three capacitors. By applying Kirchoff’s Current Law, ( KCL ) to the above circuit, we get
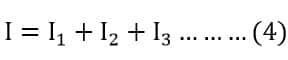
Putting the value of I1, I2, and I3 from equations 3,4 & 5 in equation 4, we get the total current drawn by the capacitors connected in parallel.
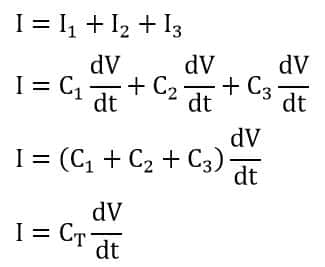
The parallels capacitance equation is;
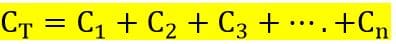
Note: The capacitance unit must be the same when adding the capacitors in parallel, If not, first convert all the capacitance values in the same unit ie. μF, nF, or pF.
We can also calculate the total capacitance of the capacitors in parallel by an alternative method of charge storage equation in a capacitor Q= CV. Here, Q is the charge in coulomb.
The charge stored on the plates of the capacitor C1 is;
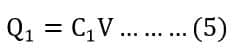
The charge stored on the plates of the capacitor C2 is;
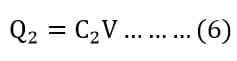
The charge stored on the plates of the capacitor C3 is;
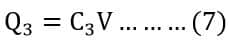
The total charge is equal to the sum of the charges stored in all three capacitors connected in parallel.
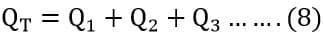
Putting the value of Q1, Q2 and Q3 from equation 6,7 & 8 in equation 8, we get
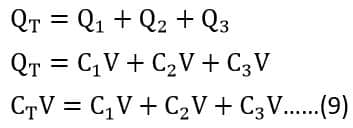
The voltage is common for all the capacitance and total capacitance, thus the voltage (V) from LHS and RHS gets canceled and we get the total capacitance equation as given below.
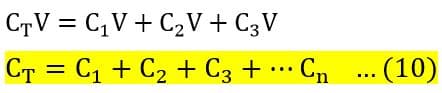
Solved Problems
Example 1– Three capacitors having capacitance values 0.5 µF,1.5 µF, and 2.0 µF respectively are connected in parallel. Find the equivalent capacitance.
Given Data-
C1 = 0.5 µF
C2= 1.5µF
C3= 2.0 µF
CT = ?
The equivalent capacitance of the above parallel circuit is;
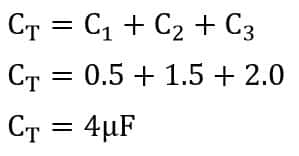
Example 2– The equivalent capacitance of three capacitors connected in parallel is 10 µF. If the capacitance value of two capacitors is 3 µF and 5.5 µF respectively, Calculate the capacitance of the third capacitor.
Given Data-
CT= 10 µF
C1 = 3 µF
C2= 5.5 µF
C3 = ?