Kirchhoff’s Current Law, KCL and Junction Rule, Solved Problems

Kirchhoff’s laws are very helpful tool for circuit analysis. It is easy to find current and voltage in a complex electrical circuit. The electrical circuit comprises of so many parallel and series resistance. Both Kirchhoff current (KCL) and Kirchhoff voltage law (KVL) are useful for finding current and voltage in a circuit. Kirchhoff’s Current Law states that the algebraic sum of current at a node or junction is zero. This law is based on the conservation of charge. KCL is also known as the node-voltage method(nodal voltage analysis).

In other words, we can say that KCL and KVL is a powerful tool to analyze the very complex electrical circuits where it is difficult to solve the circuit using Ohm’s law. 

Gustav Robert Kirchhoff in 1845 formulated Circuit laws for solving complex circuits. The law named after his name was Kirchhoff law. We call these laws as;

1. Kirchhoff’s Current Law (KCL)and
2. Kirchhoff’s Voltage Law (KVL)

Limitations of Ohms’s Law in Solving of Complex Circuit 

We can find the resistance, voltage, and current in a circuit with Ohm’s law, if out of three two electrical quantities are available. It becomes difficult to find the current and voltage in a particular circuit consist of a bridge resistance circuit or T network. We can easily find the current and voltage in such complex circuits with the use of KCL and KVL.

What is Kirchhoff’s Law?

In 1845, a German physicist, Gustav Kirchhoff developed two rules that deal with the following.

1. Conservation of current and
2. Conservation of energy

We call these laws KCL and KVL. We can find the electrical resistance, impedance, voltage, and current in a complex electrical circuit using these laws.

What do Kirchhoff’s laws state?

1. Kirchhoff’s Current Law has other names like Kirchhoff’s First Law and Kirchhoff’s Junction Rule. As per this law, the total current entering into the junction is equal to the current leaving the junction.
2. Kirchhoff’s Voltage Law has other names like Kirchhoff’s Second Law and Kirchhoff’s Loop Rule. This law states that the sum of the voltages in a closed loop is zero.

We shall discuss the current law in detail now.

Kirchhoff’s First Law – KCL

This law is based on the principle of conservation of electric charge. 

The net charge at a junction or a node of the circuit is zero. The charge cannot accumulate at a node. The charge coming at a node will go out from the same node, and thus the net charge at the node is zero.

In other words, the total current entering node or junction is equal to the current leaving the junction or node. Thus, the algebraic sum of all currents entering and leaving the junction or node is equal to zero.

The current flowing in and flowing out at a node is given below.

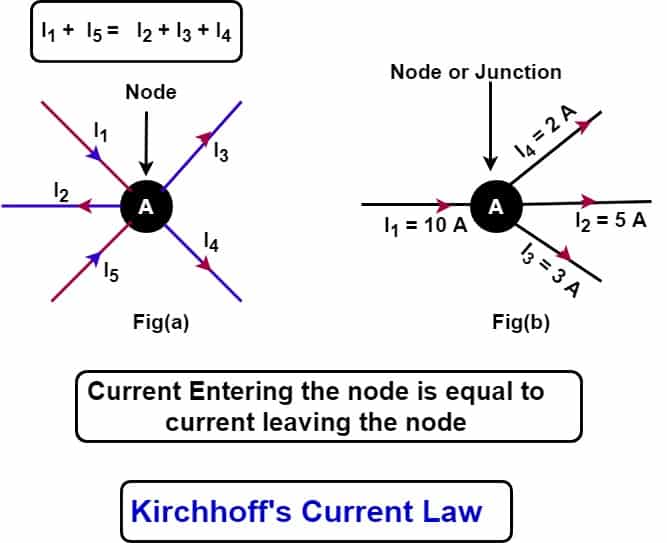
In above fig(b),

Current entering the node = 10 Amperes   ————(1)

Current leaving the node = 2 +5 +3 =10 amperes  ——(2)

The net current at the node = Current entering – Current Exit 

                                                    = 10   – 10  = 0     ———-(3

Kirchhoff’s Current Law Formula

Current Enter =  Current Exit 

Current Enter – Current Exit =0

Algebraic sum of all the current at a node is zero.

Current Notation in KCL

• Incoming current as positive if going towards a node
• Outgoing current as negative if going away from a node

As per the definition of KCL, the algebraic sum of all incoming currents towards a node and outgoing current going away from the node must be equal to zero.

I₁ + I₅ -I₂ -I₃ -I₄ = 0

I₁ + I₅ = I₂ + I₃ + I₄ 

Entering/Incoming current = Leaving/Outgoing current

Limitation of Kirchhoff’s Current Law

There are two types of circuits.

• Lumped-element model
• Distributed element model

KCL is applicable for the lumped element model where conservation of charge is possible. In a lumped element current flows in the wires and conductors. However, in distributed element model of transmission line and high-frequency circuit, the KCL rule of conservation of charge fails because of parasitic capacitance. Under parasitic capacitance, the current can even flow in the open circuit. Therefore, KCL is not applicable for high-frequency circuits.

Applications of Kirchhoff’s Current Law

• Kirchhoff’s current law is a useful tool for solving complex circuits.
• It is possible to determine the unknown value of resistance, current, and voltage.
• Kirchhoff’s current law is useful in understanding the transfer of energy in an electric circuit.
• In and out current to/from the node can be easily determined.
• KCL is applicable to almost every circuit. But, it can not be used for high-frequency circuits.

Steps of Solving Circuit Problem with KCL

1. Mark the nodes or junctions in the circuit diagram
2. Assign V₁, V₂,—V_n, etc for each node to find the voltage at every node. 
3. Find the incoming and outgoing current at each node.
4. Apply KCL to each of the nodes to set the algebraic sum of all currents into the node to zero.
5. Now, we can find the current, voltage, and resistance easily.

Solved problems on Kirchhoff’s Current Law(KCL)

In the below-given diagram, find the current through R₁ and R₂ resistance using KCL.

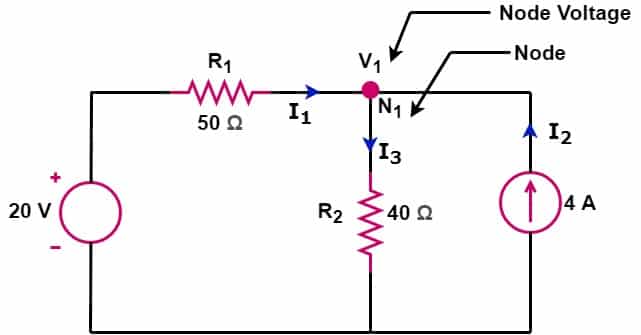
KCL at node N1

I₁ + I₂ -I₃ =0 ———–(1) 

The voltage at node N₁ is V₁, the magnitude of  I₁ and I₂ can be determined as below;

I₁ = (20-V₁)/50   ———-(2)
I₂=  4 A       —————-(3)
And,
I₃ = V₁/40    —————(4)

Putting the value of I₁, I₂ and I₃ in equation(1), we get

I₁ + I₂ -I₃ =0
(20-V₁)/50 + 4 – V₁/40  = 0
4(20-V₁) + 800 – 5V₁     = 0
80- 4V₁ +800 – 5 V₁=0
9V₁=880
V₁ = 97.78 Volts  ————–(5)

Current through Resistance R₁

I₁ = (20-V₁)/50
I₁ = (20-97.78)/50
= -77.78/50
I₁  =  – 1.5556 A

(The negative sign shows that magnitude of voltage at the node V₁ is greater than voltage source)

Current through Resistance R₂

I₃ = V₁/40 = 97.78/40 = 2.4445 A

I₁ + I₂ = I₃   ( KCL Equation for this circuit )
-1.5556 + 4  = 2.4445
4 =2.4445 + 1.5556
4 = 4 [ KCL proved]

Read Next:

• Ohm’s Law-Satatement, Formula, Solved Examples
• Why CT Secondary Shall Never Be Kept Open?
• Slip Speed in an Induction Motor
• Limitations of Ohm’s Law
• What is Millman’s Theorem? Millman’s Theorem Formula