In parallel circuits, the voltage differences across all the electrical components are equal. It means the component share the same electrical nodes. The total circuit current is equal to the sum of all the individual branch currents.
In this article, we will discuss the parallel connections of the circuit elements, and the voltage, current, and resistance of the parallel circuits. The key features of parallel circuits with respect to voltage, current, and resistance are as follows.
Voltage
The voltage across all the electrical components is equal in a parallel circuit.
Current
The current drawn by the electrical components may be equal or unequal depending on the value of the circuit resistance. Suppose, two resistance of equal value resistance connected in the parallel draw an equal current because the voltage across the nodes of the equal resistance is the same. The total circuit current can be found by adding the individual current drawn by each resistance. Thus, the total electric current is the sum of the individual branch resistances.
Resistance
The total or equivalent resistance of the parallel circuit is less than the individual branch resistances. For example, if three resistance of value 5,10 & 15 Ω resistance connected in parallel, then the total resistance of the circuit is less than 5 Ω.
Now, we will discuss the above three principles using the parallel circuit of Figure 1. The circuit has four resistances connected in a parallel combination and a battery.
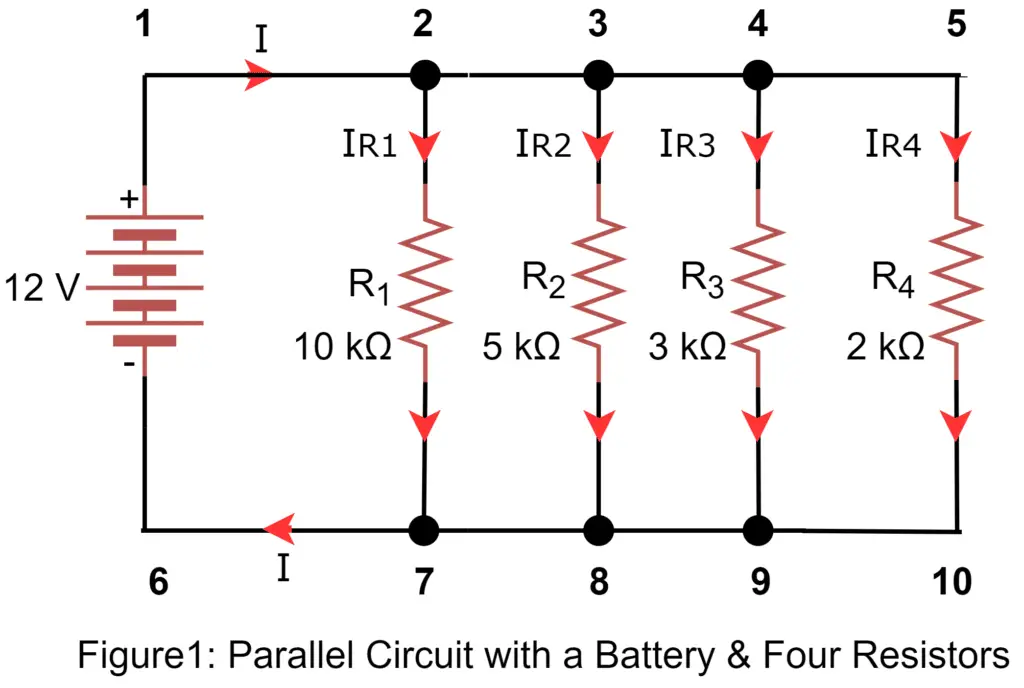
Voltage in a Parallel Circuit
The first principle of parallel circuits is that the voltage is equal across each component. When the components are connected in a parallel combination, there exist two sets of electrically common points and if we measure the voltage between a set of common points or nodes, the voltage will always be equal.
Now, if we refer to figure 1, nodes 1,2,3,4, and 5 have the same electrical potential. Similarly, nodes 6,7,8,9, and 10 are at the same electrical potential or at the same electrical nodes. Therefore, the voltage across each circuit resistance is equal to the battery voltage. The potential across nodes 1 and 6 is equal to the battery voltage and thus, the voltage across each resistance is equal to the battery voltage(12 Volts).
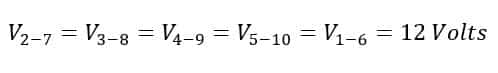
The voltage across each resistor is equal to the battery voltage.
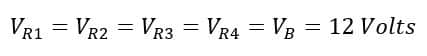
Determine Current in Parallel Circuits Using Ohm’s Law
In the circuit of Figure 1, we can find the current flowing through each resistor by applying Ohm’s Law. The voltage across each resistor is 12 volts.
The current through resistor(R1) is;
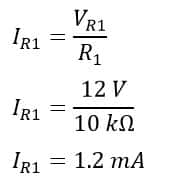
The current through resistor(R2) is;
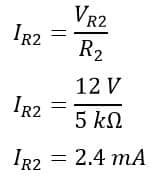
Current through resistor(R3) is;
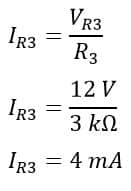
The current through resistor(R4) is;
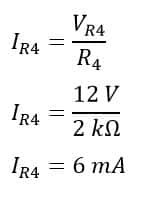
However, at this point, we still need to calculate the total current or total resistance for this circuit. It is clear that the total current must be equal to the sum of individual branch current.
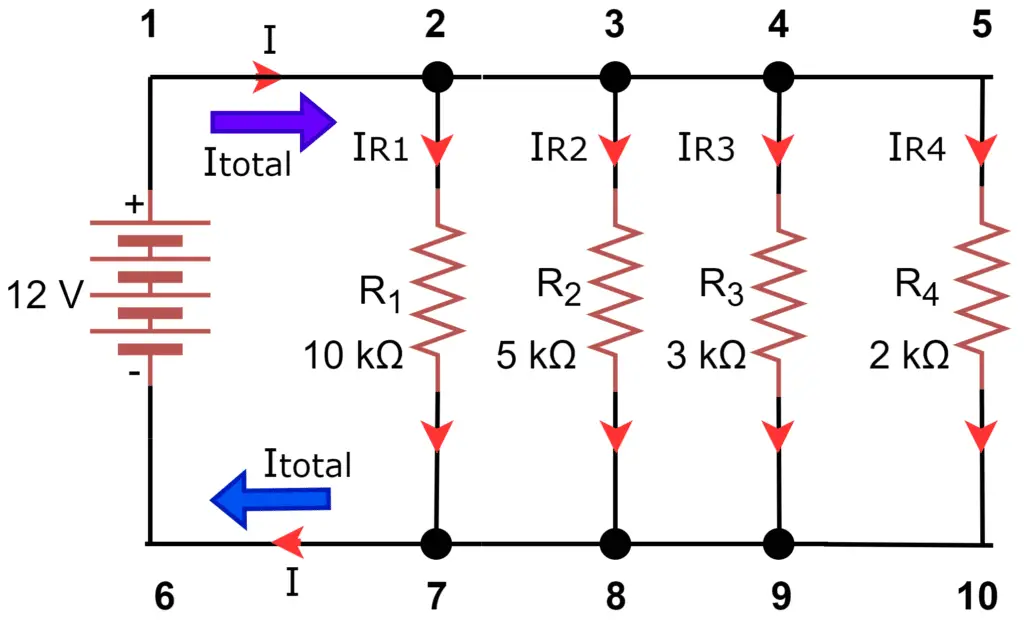
The total circuit current exists from the positive (+) battery terminal at node 1 and travels through the circuit, some part of the total current diverts at node 2 and passes through the resistor R1, some more current diverts at point 3 and pass through the resistor R2, and some current diverts at node 3 and pass through the resistor R3, and the balance current goes through R4. The process is like branching off the main river into several smaller streams, and the total flow rates of all streams must equal the flow rate of the main river.
The individual branch current again meets at node 7 which is equal to the sum of the current flowing through resistors R1, R2, R3, & R4, The total current rejoins at node 7 and it flows back to the battery’s negative terminal (-) toward point 8.
The same thing is encountered where the currents through R1, R2, and R3 rejoin to flow back to the battery’s negative terminal (-) toward point 8. The current flow from point 7 to point 8 must equal the sum of the branch currents through R1, R2, and R3.
Thus, the total current in the parallel circuit is;
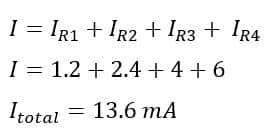
How to Calculate Total Resistance in a Parallel Circuit?
We can calculate the total effective resistance if the voltage and the total current data are available. By applying Ohm’s law, you can find the total effective resistance.
The total current and voltage are 13.6 mA and 12 volts respectively. Therefore, the total effective resistance of the parallel circuit is;
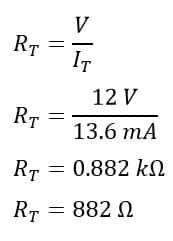
If you observe this total effective resistance value, it is less than any one of the individual resistors( 10kΩ,5kΩ,3kΩ and 2kΩ). Here, we can conclude that the total resistance of the parallel circuit is always less than the value of any one of the individual resistors.
In the series circuit, the total effective resistance is always more than any one of the individual resistors.
But, the opposite is true in the case of the parallel circuit. The reason behind this is that each resistor connected in the parallel combination reduces the total equivalent or effective resistance. The relationship between effective resistance and individual resistance in a parallel circuit can be expressed by the following mathematical formula.
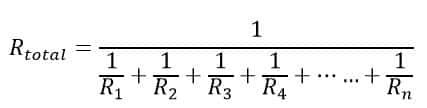
The conductance of the circuit is reciprocal to the resistance. The conductance of a parallel circuit is equal to the sum of the individual branch conductance. The calculation becomes easier with the calculation of conductance in the parallel circuit.
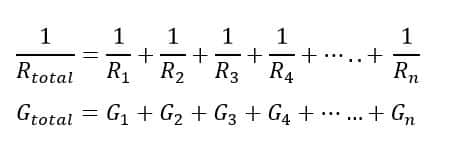
Summary of Parallel Circuit Fundamentals:
- The voltage is the same for all electrical components in a parallel circuit:
- V1 = V2 = V3=V4. . . Vn
- The total current in the parallel circuit is the sum of the individual branch currents:
- Itotal = I1 + I2 + I3.+I4 . . In
- The total effective resistance of a parallel circuit is less than any of the individual branch resistances.