In this article, we will solve the Unsolved Problems from BL Theraja Vol-1-Tutorial Problems No. 1.1 for better understanding of electrical resistivity.
Problem-1 Calculate the resistance of 100 m length of a wire having a uniform cross-sectional area of 0.1 mm2 if the wire is made of manganin having a resistivity of 50 × 10−8 Ω-m. If the wire is drawn out to three times its original length, by how many times would you expect its resistance to be increased ?
Solution:
R = ρ L / A (1)
Where,
R = resistance of the conductor (ohms, Ω)
ρ = resistivity of the conductor material (ohm metre, Ω-m)
L = length of conductor (m)
A = cross-sectional area of conductor (m2)
According to the given data, we have,
L= 100 m, A=0.1 mm2, ρ= 50 x 10-8 Ω m
R = 50×10-8 ………………………………. (from equation 1)
= 50×10-8x102x107
R = 50×10-8x109
R = 500 Ω
Now, according to question if the wire is drawn out to three times its original length
The new length becomes,
L’ = 3L
As we know that Volume can be defined as, (Area of cross section multiplied by Length), and here the volume will remain same and hence this can be expressed as
V= AxL = A’x3L
A= 3A’
A’=A/3
Therefore, from equation 1,
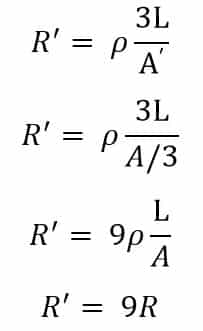
Thus, the resistance will increase by 9 times.
Problem-2 : A cube of a material of side 1 cm has a resistance of 0.001 Ω between its opposite faces. If the same volume of the material has a length of 8 cm and a uniform cross-section, what will be the resistance of this length?
Solution:
R = ρ L / A (1)
Where,
R = resistance of the conductor (ohms, Ω)
ρ = resistivity of the conductor material (ohm metre, Ω m)
L = length of conductor (m)
A = cross-sectional area of conductor (m2)
According to the given data,
L= 1 cm, R= 0.001 Ω (2)
R = ρ
As Volume is same and we know volume can be calculated by multiplying Area of cross section (A) and Length (L)
Hence,
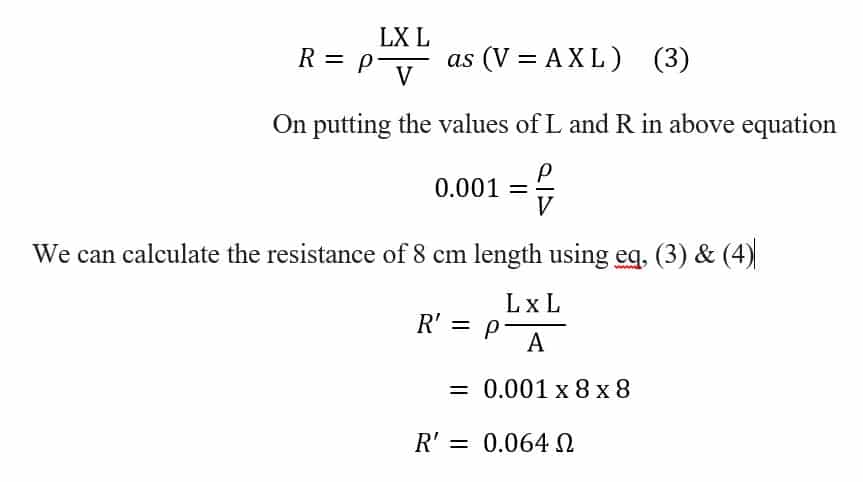
R’ = 0.064 Ω
Problem-3 : A lead wire and an iron wire are connected in parallel. Their respective specific resistances are in the ratio 49 : 24. The former carries 80 percent more current than the latter and the latter is 47 percent longer than the former. Determine the ratio of their cross-sectional area.
According to the data given in question,
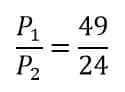
And now question is saying former (I1) carried 80 % more current than the latter (I2)
That means,
If, I2 = 1 A
Then, I1 = 1.8 A
Similarly for the length,
If, L1 = 1
Then, L2 = 1.47
Now,
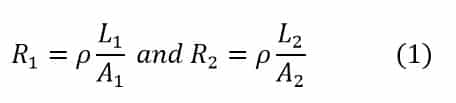
And as the lead wire and iron wire connected in parallel. By using current division rule,
I1 = V1/ R1 and I1 = V2/R 2 (2)
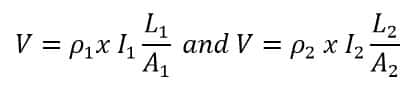
By equating above,
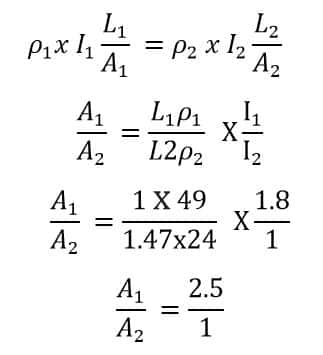
Problem-4 : A rectangular metal strip has the following dimensions : x = 10 cm, y = 0.5 cm, z = 0.2 cm Determine the ratio of resistances Rx, Ry, and Rz between the respective pairs of opposite faces.
Solution:
As we know the Relation between resistance to its resistivity and dimensions can be calculated by using formula,
R = ρ L / A
According to the question,

Problem-5 : The resistance of a conductor 1 mm2 in cross-section and 20 m long is 0.346 Ω. Determine the specific resistance of the conducting material.
Solution:
R = ρ L / A (1)
Where,
R = resistance of the conductor (ohms, Ω)
ρ = resistivity of the conductor material (ohm metre, Ω m)
L = length of conductor (m)
A = cross-sectional area of conductor (m2)
According to the given data, we have,
L= 20 m, A=1 mm2, R= 0.346Ω
By using equation 1,
R = ρ L / A
ρ = RA / L
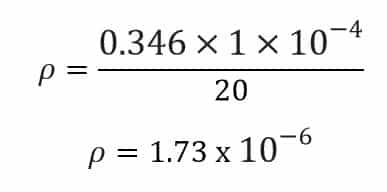
Specific resistance of the conducting material is, ρ = 1.73 x 10-6 Ω m
Problem-6 : When a current of 2 A flows for 3 micro-seconds in a copper wire, estimate the number of electrons crossing the cross-section of the wire.
Solution:
Given,
Current through the wire is, I = 2 A
Time taken for this current flow, t = 3 µ s
t = 3×10-6 s
Assume,
n = number of electrons that crossed the cross section of wire in time t
e = Charge of the electron
So, the total charge in wire can be calculated as
q = ne (where, q is total charge) (1)
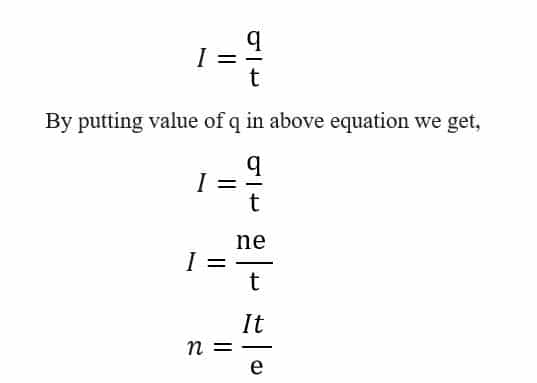
Putting the values in above formula,
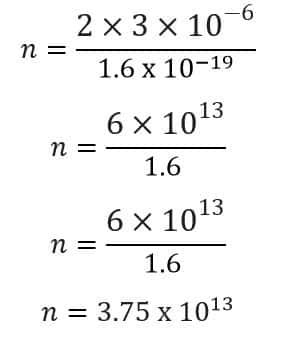
Therefore, the number of electrons crossing the cross-section of the wire is 3.75 x 1013.
Read Next :
Excellent Job Sir !
I love your effort. Thanks a million