Transformers are always rated in kVA (kilovolt-amperes) rather than kW (kilowatts) because their design is based on voltage and current capacity, not the power factor of the load. Power factor varies with the type of load, so kVA is a more universal and practical unit for transformer rating.
This means that whether a transformer is feeding a purely resistive heater, an induction motor, or a mix of both, the kVA rating still correctly defines its safe operating limit. In contrast, kW ratings would be different for each case, making the specification less versatile.
Understanding the Basics of Transformer Ratings
Transformers are rated in kVA (kilovolt-amperes), not in kW (kilowatts), because kVA represents the apparent power—the combination of active power (kW) that actually performs work and reactive power (kVAr) that sustains magnetic and electric fields in inductive or capacitive loads.
This makes kVA a universal rating, valid for both resistive and inductive loads, regardless of their power factor.
The main limitation of a transformer is the maximum voltage and current its windings can safely carry without overheating. This voltage-current combination determines the apparent power the transformer can handle, which is expressed in kVA.
For example, a purely resistive heater has a power factor of 1, so its kW output equals the transformer’s kVA rating. In contrast, an induction motor might have a power factor of 0.8, so the same transformer delivers fewer kW even when operating at its full kVA capacity.
Because manufacturers cannot predict the exact power factor of every user’s load, they specify transformer capacity in kVA. This ensures the transformer rating remains valid for all types of loads and allows flexibility in operation, making kVA the standard unit for transformer ratings worldwide.

Why Transformer Rating in kVA, Not in kW
The power factor at the transformer’s secondary and primary is equal to the combined power factor of all electrical loads connected to the transformer.
Thus, the transformer does not have a fixed power factor, and the power factor varies with the types of load connected to it and also on the percentage loading on the transformer.
Since the transformer itself does not consume significant active power (except for small core and copper losses), its rating needs to reflect total apparent power flow, not just the active portion.
Transformer as a Power Link
The transformer is a link between the alternator and the load. The alternator supplies active and reactive power to the load. Similarly, the transformer is a power supply source that supplies the active kW and reactive kVAR to electrical loads.
The volts x Amps equation of the transformer gives the maximum current that the winding can carry. The transformer winding can’t carry current more than its rated current carrying capacity. The same kVA and more MVA mean winding can carry more current without overheating.
This also explains why generators are rated in kVA for similar reasons — they, too, must deliver both kW and kVAr to the load without being tied to a specific power factor.
Why Not Rate the Transformer in kW?
If the transformer is rated in kW, the designer has to fix the kVAR capacity of the transformer. However, kVAR depends on the types of loads connected to the transformer, and it is not possible to fix the kVAR delivering capacity of the transformer.
In other words, if the transformer is rated based on KW, the user has to operate the transformer at the designed power factor of the transformer.
However, it is not practical to operate the transformer at a particular power factor or a particular kVAr because the load power factor varies, and the system power factor changes with variation in the power factor of the connected loads.
Flexibility in Operation
The transformer designer does not know at what power factor the customer will operate the transformer. The designer gives the choice to operate the transformer at whatever power factor by rating the transformer in apparent power (KVA or MVA).
This approach also makes procurement easier, as a single 100 kVA transformer can be used across many industries without the manufacturer needing to know the exact load conditions
Mathematical Relation Between kVA, kW, and kVAr
The apparent power(kVA) of the transformer is equal to the vector sum of active power(kW) and reactive power(kVAr).
kVA⃗= kW⃗+ kVAr⃗
kVA2= kW2 + kVAr2
kVA =√(kW2 +kVAr2) ——–(1)
Where,
kVA – Apparent Power
kW – Active Power
kVAr – Reactive Power
From equation(1), if the load is resistive, then the power factor is unity, and kVAr =0
kVA = kW ( if the load is resistive)
This formula is key to understanding transformer ratings — it clearly shows why the kVA remains the same, even though the kW output changes with power factor.
If the power factor is low, the kVAR supplied by the transformer will increase, and correspondingly, the active power delivery will decrease. The transformer will be underutilized if the power factor of the loads is low.
Quick Table: Effect of Power Factor on Transformer Capacity
| Power Factor | kW Output from a 100 kVA Transformer |
| 1.0 | 100 kW |
| 0.9 | 90 kW |
| 0.8 | 80 kW |
| 0.7 | 70 kW |
This shows why kVA is used — the same transformer can handle different kW outputs depending on power factor.
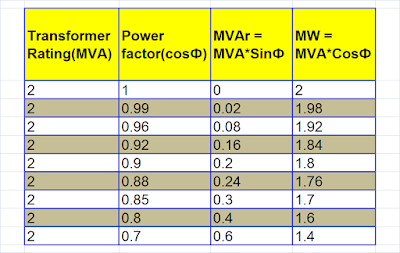
From the above table, it is clear that the active power delivering capacity of the transformer gets lowered with a lower power factor.
In practice, many industries install power factor correction capacitors to keep the transformer operating closer to its maximum kW potential.
Improving Transformer Utilization
To fully utilize the transformer, the power factor should be high. The better the power factor, the lesser the kVAr demands by the electrical system, and thus, the transformer’s active power-delivering capacity can be increased.
The power factor can be improved by installing capacitor banks to neutralize the reactive kVAr with capacitive kVAr.
To fully utilize the transformer, the power factor should be high. The better the power factor, the lesser the kVAr demands by the electrical system, and thus, the transformer’s active power-delivering capacity can be increased.
The power factor can be improved by installing capacitor banks to neutralize the reactive kVAr with capacitive kVAr.
In some modern facilities, automatic power factor correction panels are used to adjust capacitive compensation dynamically as loads change throughout the day.
Advantages of Rating Transformers in kVA
- Universal applicability – Works for both inductive and resistive loads without changing the rating.
- No fixed PF assumption – The rating remains valid regardless of load power factor.
- Flexibility – Suitable for a wide variety of load types and operating conditions.
Conclusion
Transformers are rated in kVA because this rating remains valid for any power factor. This ensures flexibility for the end-user, prevents underutilization due to load variations, and allows the same transformer to handle both resistive and inductive loads efficiently.
So, whether it’s a welding shop with fluctuating loads, a data center with mostly resistive loads, or a factory full of motors, the same transformer rating system works universally — and that’s why transformer is rated in kVA.
Related Articles:
HOW CAN I GET THE PDF ON THIS TOPIC
Very good knowledge sir
Aap ke es matter se bahut knowledge mila
Very very thanks