Uncertainty Calculations of Thermal Calibration

In this article, we will discuss the Uncertainty Calculations of Thermal Calibration. Uncertainty means how uncertain or certain we are about the result. No measurement is complete without uncertainty. 

What is Uncertainty?

Uncertainty is the quantification of the level of doubt we have about any measurement. Uncertainty means how certain or uncertain we are on measured readings. No reading is 100% accurate. It has some level of uncertainty present.

Uncertainty includes many factors like personal Skill, resolution of the instrument, the accuracy of the instrument, etc.

There are two types of Uncertainty – Type A and Type B uncertainty

Type A Uncertainty

• The Type A evaluation of standard uncertainty is the method of evaluating the uncertainty by the statistical analysis of a series of observations.
• Type A uncertainty is based on readings taken during calibration.

Type B Uncertainty

• The Type B evaluation of standard uncertainty is the method of evaluating the uncertainty by means other than the statistical analysis of the repeat measurements
• Type B uncertainty is based on other factors than readings taken during calibration.

Uncertainty Components of Temperature Calibration to be considered, but not limited to:

Type A

1. Repeatability
2. Reproducibility

Type B

1. Uncertainty due to Standard equipment (Temperature Sensor and Indicator)
2. Accuracy of Standard equipment (Temperature Sensor and Indicator)
3. Stability of Temperature Source
4. Uniformity of Temperature Source
5. Resolution of readout
6. Uncertainty of readout unit in case of sensor calibration

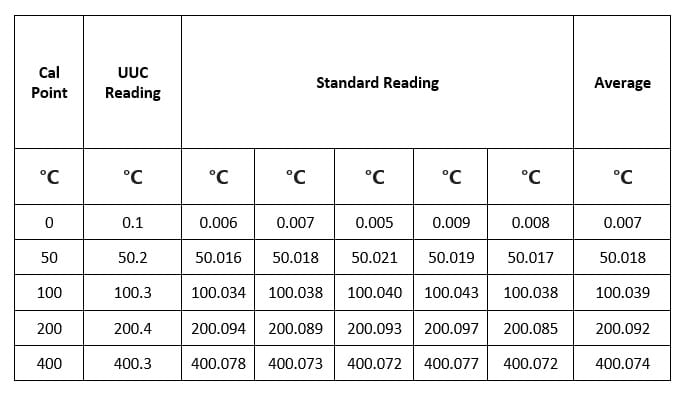
Example– Calibration of Temperature Sensor with Indicator

Uncertainty Calculations of Thermal Calibration.

Consider UUC Temperature Sensor with Indicator of range 0 to 400 °C with resolution 0.1 °C calibrated with 4 wire master RTD Sensor (Class A) with 6.5 DMM with resolution 0.001 °C. Uncertainty of master RTD Sensor is 0.07°C and 6.5 DMM is 0.03°C with K=2.

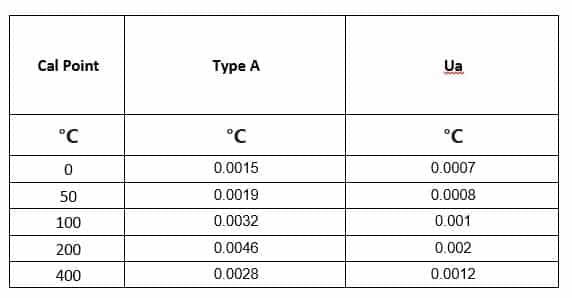
Type A Uncertainty

Type A uncertainty is the standard deviation of readings.

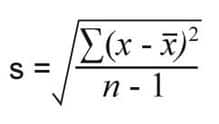
Where:
x:  reading
`x : Mean (average)
n: no of readings i.e. 5 in the above case
Using excel in can be calculated using formula = STDEV ()
Uncertainty due to standard deviation (U_a )= S.D / sqrt (n)
Sqrt: square root

Type B Uncertainty–(Uncertainty Calculations of Thermal Calibration)

Uncertainty due to Standard equipment

1. Uncertainty due to RTD Sensor
2. 6.5 DMM(Indicator) uncertainty

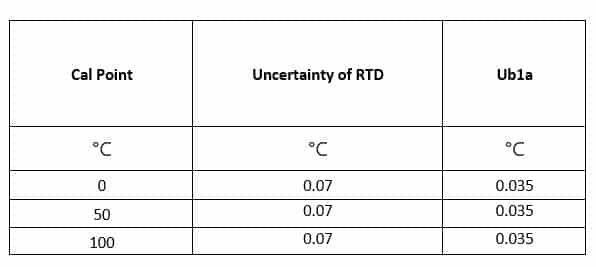
Standard equipment uncertainty is mentioned on the calibration certificate. Also, the K value is mentioned in the calibration certificate.

Uncertainty due to Standard equipment (U_b1) = Uncertainty of standard equipment/ k

Here, in our example Uncertainty of RTD Sensor is 0.07°C and K value is 2, Uncertainty of Indicator is 0.03°C and K value is 2

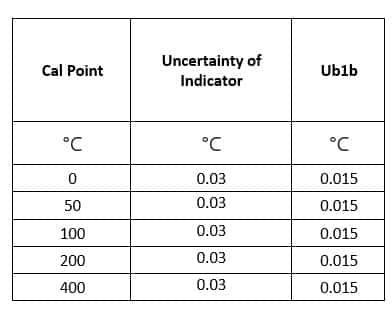
Uncertainty due to Accuracy of Standard equipment

1. Accuracy due to RTD Sensor
2. Accuracy due to 6.5 DMM(Indicator)

Uncertainty due to Accuracy of Standard equipment (U_b2) =
Accuracy of standard equipment/ Sqrt (3)

Assuming rectangular distribution, the value obtained is divided by a square root of 3.

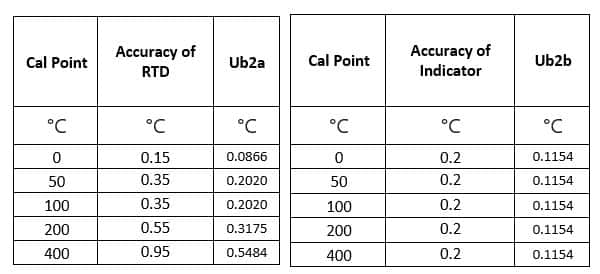
Uncertainty due to Stability

Stability of Temperature Bath is 0.1°C

Uncertainty due to Stability (U_b3) = Stability/ Sqrt (3)

Uncertainty due to Uniformity

Uniformity of Temperature Bath is 0.3°C

Uncertainty due to Uniformity (U_b4) = Uniformity/ Sqrt (3)

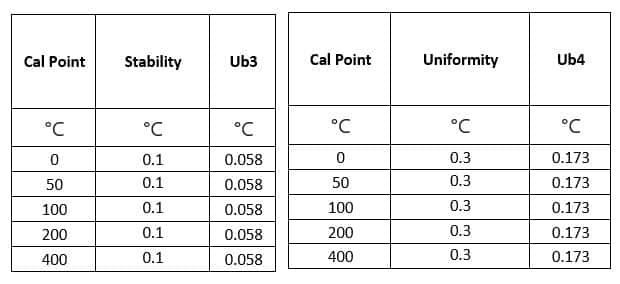
Uncertainty due to Resolution-(Uncertainty Calculations of Thermal Calibration)

If UUC set according to calibration point, and Standard reading changes, we consider the resolution of Standard.

If Standard is set according to calibration point, and UUC readings are changed, resolution of UUC is considered.

For example, UUC is set and Standard readings are changing,

Therefore, the Resolution of the standard is considered.

Resolution of Standard is 0.001 °C

Uncertainty due to Resolution (U_b5) = ((Resolution /2)) / SQRT (3))

Assuming rectangular distribution, value obtained is divided by square root of 3.

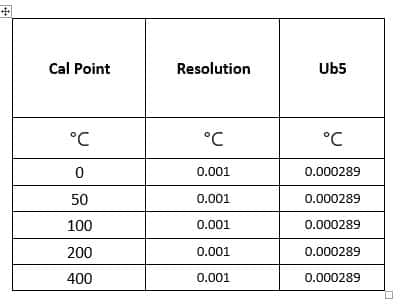
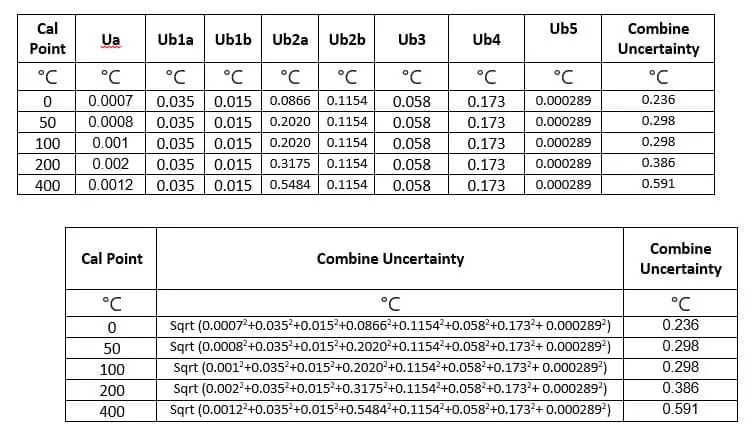
Combined Uncertainty

Combined uncertainty is not simple addition. To combine all components, Units of all Components should be the same for addition. If not, use the proper conversion formula to make all components in the same units. Or else the % value can be used.

Step 1:

All individual uncertainty U_a, U_b1, U_b2, U_b3, U_b4, U_b5  are squared.

Step 2:

All individual uncertainty is added after squaring

Step 3: 

The square root of the value is obtained in Step 2.

Combined Uncertainty is also called Standard Uncertainty

Effective degrees of freedom

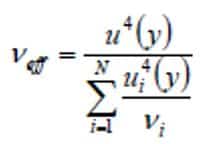
Expanded Uncertainty

Standard Uncertainty is multiplied by the k factor to obtained Expanded Uncertainty. Where k is the coverage factor corresponding to the effective degree of freedom. k factor is 2.

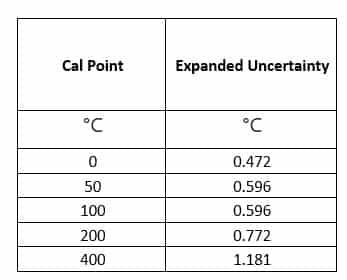
Expanded uncertainty is reported in the calibration certificate

A similar type of calculation is done for temperature Sensors without an Indicator.

Uncertainty Component of readout is included in case of only sensor calibration (i.e. Without Indicator)