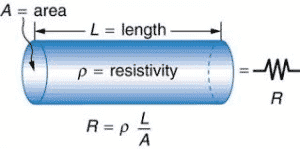
We shall understand with an example how the resistance of a wire changes with stretching its length.
Example-1 –Change of Electrical Resistance with wire stretching
The resistance of L length wire is R. If half of its length stretch such as the total length becomes 2L what will be the final resistance?
The resistance of L length wire is R.
The resistance of L/2 length wire is R/2
Now the other L/2 length of the wire is stretched to length X to have full length of conductor 2L
L/2 +X = 2L
X= 3/2 L
The length of the stretched conductor is 1.5 L.
Length of conductor L/2 is stretched up to 1.5 L, the length of the stretch conductor is now 3 times of the original length hence the diameter of the conductor is d/3. The resistance of the stretched conductor.
R1= ⍴ x L/A
= ⍴ x L/πd2
= 3 /(1/9)
R1= 27 times of the original resistance of the half length wire
R1= 27 x R/2 =13.5 R
The resistance of conductor after stretching is
= R/2 + 13.5 R=
= 14 R
The new resistance of the wire after stretching its half length is 14 times of the original resistance of conductor.
Example-2
What is the new resistance of a wire if it is stretched to twice its original length. Original resistance is 10 ohm.
After stretching of wire
Length of wire L1 = 2 L
New Area A1 = A/2
In above conditions,the volume of the wire remain the same.
New Resistance R1 = ρ L1 /A1
= ρ x 2L /A/2
= ρ x 4L /A
R1 = 4 ρ L /A
= 4 R = 4 x 10
R1 = 40Ω
New resistance will be 4 times of the original resistance
Example-3
A wire has a resistance of 30 ohms. We stretch the wire by 10% of its original length, what will be the new resistance?
Let the original length and area of a wire is L and A respectively.
The resistance of wire R = ρ L /A
After 10 % stretching the length and area of wire is L1 and A1
L1 = 1.1 L
The volume must remain the same after stretching
A1 = (1/1.1 )A = 0.909 A
The new resistance of wire
R1 = ρ L1/A1
= ρ (1.1L)/ (0.909 A)
R1 = 1.21 ρ L /A = 1.21R
= 1.21 x 30
R1 = 36.3 Ω
The above illustrative examples shows how the resistance of a wire changes with stretching its length.
Related Post