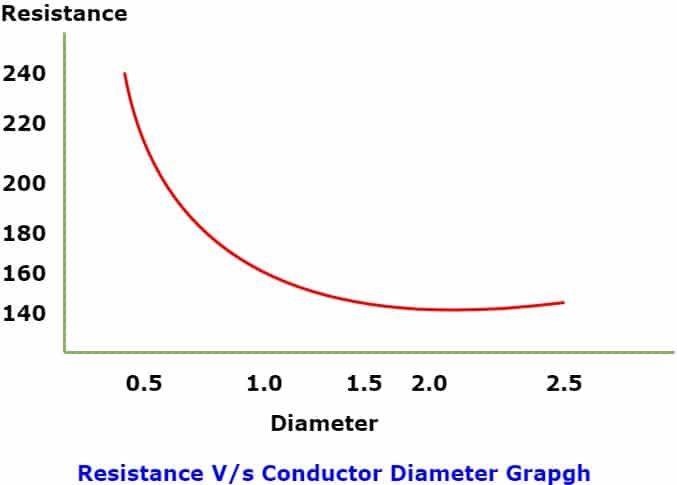
In this posts we shall study how does resistance vary with diameter.The resistance is inversely proportion to the area of the conductor.The area is proportional to the square of the diameter.Therefore, the resistance is inversely proportional to the square of the diameter of the conductor.
The area of a circular conductor is A= πD2/4
The resistance gets decreased as the diameter is increased.
If ratio of resistance of the conductor of the same length and diameter ratio is 1:2 will have resistance ratio 4:1.
Resistance depends on the material and its shape
The resistance depends on;
- Shape of the object – Length and cross section area
- Material property
We can calculate the resistance of cylindrical resistor as follows.
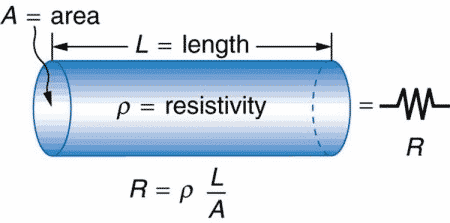
Here,
L = Length of the cylindrical conductor
A = Its Cross Section Area
The resistance of conductor can be expressed by following mathematical expression.
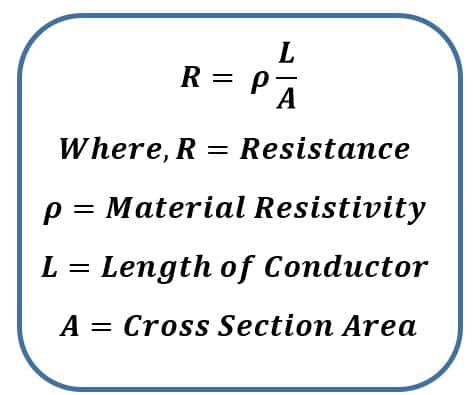
The resistivity is constant for each conducting materials and it does not change if the temperature is kept constant. The physical dimensions of conductor- Length and cross section area affect the resistance of the conductor. Let us understand how the resistance changes with change in length or cross section area.
The resistance of the conductor depends on easiness of flow of electrons. The less the hindrance to flow of electrons, the lesser is the resistance.
If the length of the conductor increases, the electrons collide more frequently from the walls of a conductor. This cause resistance to flow of electrons. Therefore, with increase in the length of conductor, its resistance increases.
In a similar way, if the cross section area of the conductor is more, the electrons find easy path without collision to each other.
Example
A filament lamp made of tungsten is cylindrical in shape, and has cold resistance 0.50 Ω. The length of filament is 5 cm long. What is its diameter?
R = 0.5 Ω
L = 5 cm
ρ = 5.60×10−8 Ω-m
R = ρ L/A
A = ρ L/A
= 5.60 x 10-8 x 5 x 10-2 /0.5
A = 5.6 x 10-9
The area of a circular conductor is A= πD2/4
D =√(4A/π)
= √(4 x 5.6 x 10-9 /π)
= √(71.3 x 10-10 )
D = 2.17 x 10-5
Diameter of conductor V/s Resistance Graph
R = ρ L/A ——-(1)
A = ρ L/A ——–(2)
A= πD2/4 ——(3)
Putting value of equation(3) in (1);
R = ρ L/A
= ρ L/(πD2/4)
= 4 ρ L/πD2
R = K/D2
Where, K( Constant)=4 ρ L/π
| R ∝ 1/ D2 |
| D ∝ √(1/R) |
From below graph it is clear how the Resistance vary with diameter.