Though all orders of harmonics harm an electrical power system, the 5th and 7th order harmonics are more harmful to electrical networks. One solution to mitigate these lower-order harmonics is to install harmonic filters. We will discuss the criteria for harmonic filter selection in detail.
The harmonic filters can be categorized into three categories, i.e., passive filters, active filters, and hybrid filters. The passive filter has passive components like a resistor, inductor, and capacitor. The active filter is designed using semiconductor devices like IGBTs.
Hybrid filters are a combination of active and passive filters. For the cost-effectiveness of the installation, the hybrid filters are used to mitigate the lower-order harmonics using the passive filters and the higher-order harmonics using the active filters. A combination of active and passive filters is known as a hybrid filter.
The passive filters can be further categorized into tuned and de-tuned filters. The frequency of the 5th and 7th-order harmonics is 250 Hz and 350 Hz, respectively. The passive filters are generally used to mitigate 5th and 7th-order harmonics because the magnitude of lower-order harmonics’ current is greater than that of higher-order harmonics.
Tuned Harmonic Filter Selection
A tuned filter works on the principle of providing the least impedance path for one or two harmonic frequencies and has a tuning frequency that is within +/- 10 % of the harmonic frequency to be filtered. Tuned filters of particular harmonics order carry more harmonic current as they offer low impedance to the dominant harmonics.
Therefore, the tuned filter design has to be done carefully. The tuned filter is formed with a combination of inductance and capacitance, so they are bulkier than the de-tuned and active filters.
The tuned filters can be installed only after a detailed harmonics study. Inherently, tuned filters do not adapt quickly to changes in power network configuration, and their efficiency is usually altered when network configuration changes.
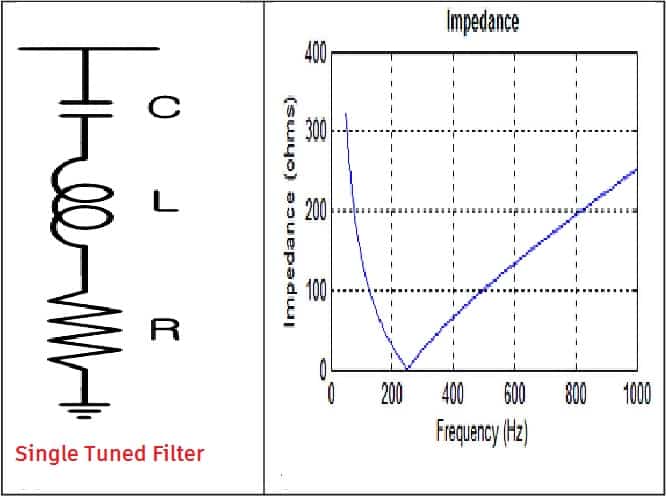
Whenever new non-linear loads get added to the network after the installation of the filters, harmonics studies are again required to be carried out. Several tuned filters are to be used in parallel if more than one harmonic frequency is to be filtered. The self-resonance frequency is related to the tuning factor, which is defined as the ratio of the inductive to capacitive reactance of the filter expressed as a percentage.
The major problem with tuned filters is that if the inductive reactance of the electrical network is equal to the capacitive reactance of the system, the resonance phenomenon occurs. The resonance phenomenon can cause the failure of the power factor correcting capacitors.
De-tuned Harmonic Filter Selection
To solve this resonance issue, the filter is deliberately tuned for a particular harmonic frequency. For example, the filter for 5th-order harmonics current is designed for a frequency lower than 250 Hz. With detuning, some percentage of the harmonics current remains unfiltered, but the resonance can be avoided.
The tuning factor can be given to the tuned filters to avoid the resonance problem. The following mathematical expressions give the tuning factor and tuning frequency of the harmonic filter:
Tuning factor, p (%)
=[(Inductive reactance) / ((Capacitive reactance)] x 100
= (XL/XC )*100
Tuning frequency of the filter,
Fr=Fs/√0.01p Hz (P is in percentage)
For 5 % detuning Fr=50/√ 0.05 = 224 Hz
Where fs = Fundamental system frequency
Filter frequency with de-tuning
| De-tuning Factor (%) | Filter Frequency (Hz) |
| 5 | 224 |
| 7 | 189 |
| 8 | 177 |
| 14 | 134 |
Active Harmonic Filter
The PWM INVERTER technology is the basic building block of an Active Harmonic Filter. Active filters are new-generation harmonic filters that use modern technologies and devices to provide revolutionary filtering solutions.
The active filter produces the harmonic currents spectrum in phase opposition to that produced by the non-linear loads, and these generated harmonic currents of the active filters are injected into the system in real time to ensure the effective cancellation of all harmonics present in the network.
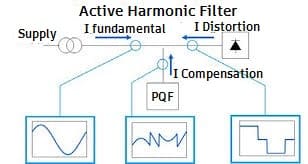
In addition to canceling the harmonic current, an active filter also improves the power factor by providing both capacitive and inductive reactive power in a step-less manner. Active filters are the most technologically advanced solutions available for harmonic filtering.
The active filter uses a CPU to detect the order and magnitude of the harmonics present in the network. It generates a harmonic current spectrum in phase opposition to the measured spectrum.
Informative article