Power cables carry power from the supply source to the load point. They have DC resistance, which depends on their size. When current flows through the cable, heat loss, I2R, occurs. The heat loss in the cable is proportional to the square of the current flowing through the cable and proportional to the cable resistance. The harmonic current causes additional heating in the power cable due to increased I2R losses.
The DC resistance of the cable does not change if the cable carries the DC power. However, in the case of AC power transmission, the resistance increases with an increase in the frequency and also an increase in the current. The AC resistance of the cable is higher than the DC resistance of the cable. Thus, the power loss caused by the heating of the cable increases if the cable carries high-frequency AC.
Table of Contents
Effects of Harmonics on Power Cables
The flowings are the adverse effect of the harmonics on the power cables.
- Increased I2R Loss
- Increased RMS Current and Losses
- Overvoltage
- Derating of Cable
Increased I2R Losses due to Harmonics
The RMS value of the current increases when the magnitude of the harmonics current increases. In the harmonic-rich supply system, the cable losses increase for two reasons.
- Increase in the cable resistance with harmonics.
- Increase of RMS current due to Harmonics
Increased RMS current due to Harmonics
The harmonic current waveform is not sinusoidal. According to the Fourier series, the non-sinusoidal waveform can be resolved into sinusoidal and integral multiples of the sinusoidal waveform. The integral multiples of the fundamental frequency are known as harmonics. For example, take a nonsinusoidal current waveform as given below.
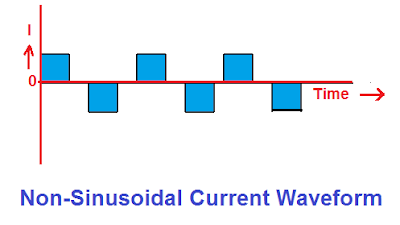
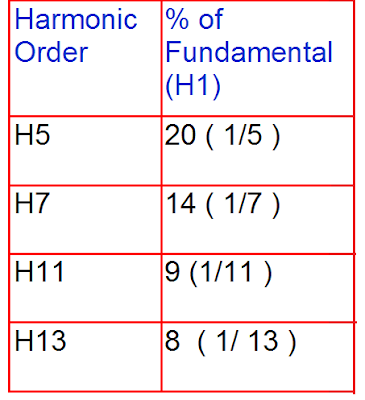
This sort of current waveform contains harmonics. If we synthesize this waveform, the magnitude of the harmonics is as follows.
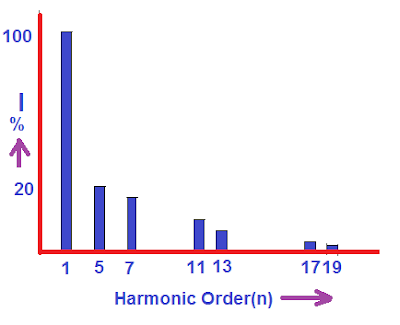
The harmonic spectrum of the current waveform is given below.
The RMS value of the non-sinusoidal current waveform can be calculated by taking the harmonic current into account.
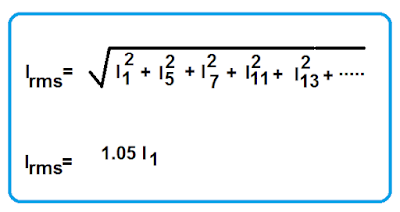
Where,
I1 = fundamental current
I5 = 5th harmonic current
I7 = 7th harmonic current
I11= 11th harmonic current
The RMS value of the current increases by 5 % of the fundamental RMS current. If the fundamental current is 100 amperes and the load draws harmonic current from the supply source, the total current flowing will be 105 amperes. Increased current due to harmonic current causes a 10% additional power loss in the cable. The power cable must be de-rated according to the harmonic current flowing through the cable.
While selecting cable for a particular load, the harmonic current must be considered.
The other factor contributing to the increase in power loss is the AC resistance of the cable. The harmonic current has a higher frequency -250 Hz, 350 Hz,550 Hz, etc. At higher frequencies, the current tends to flow on the outer surface of the conductor. The phenomenon is called the SKIN EFFECT. The effective resistance increases when the power cable carries the high-frequency current. The AC resistance of the power cable is always more than the DC resistance because of the skin effect and the proximity effect. The skin effect is proportional to the frequency, and the proximity effect is proportional to the square of the frequency. Thus, the effective resistance of the conductor carrying harmonic current increases.
Over Voltage due to Harmonics
If the capacitor banks installed for power factor correction resonate with the inductance of the transformer, the resonance phenomenon can boost the system voltage. In this condition, the power cables experience voltage stress, and the cable insulation may fail.
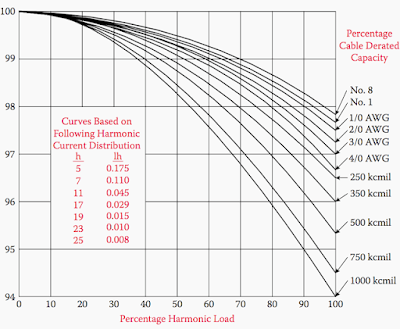
Cable Derating
The heating effect due to harmonic current must be considered while sizing the cable. The usual derating curves, as per IEEE519, have been plotted for a number of cable sizes for 6-pulse harmonic distribution.
1 thought on “Effects of Harmonics on Power Cables”