Eddy Current Loss Formula Derivation

The Eddy Current Loss Formula Derivation is an essential concept for understanding how energy is lost as heat in conductors subjected to varying magnetic fields.

What is Eddy Current Loss?

When the conductor is placed in the varying magnetic field, the localized current starts flowing in the conductor, which is called the eddy current.

The energy loss wasted in the form of heat energy in the conductor caused by the flow of eddy current is known as eddy current loss.

The eddy current loss can be minimized using thin laminated silicon steel sheets instead of solid steel sheets. The various factors like magnetic flux density, frequency, electrical properties of the material, and thickness of the laminated sheets affect the eddy current loss.

The derivation of the eddy current loss formula gives an in-depth overview of the factors on which eddy current loss depends. The formula of the eddy current loss(P) is given below.

Let us derive the formula of the eddy current loss for a better understanding of the eddy current loss in a steel core.

Step-by-Step Eddy Current Loss Formula Derivation

To better understand eddy current loss, let us derive the formula for a steel core:

With thin laminated sheets, the area of the eddy current path reduces, and thus, the path’s resistance gets increased. With an increased resistance, the potential developed at two points of the lamination gets lowered.

As a result, the magnitude of the eddy current decreases, leading to a reduction in eddy current loss.

Derivation for Thin Laminated Sheets

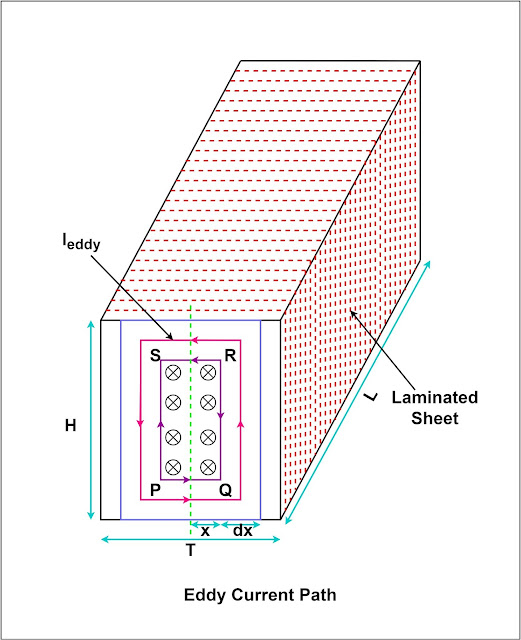
Let the length, height, and thickness of the laminated sheet be L,h, and𝞃 respectively. The thickness of the sheet 𝞃 is very very less than the length(L) and height(h) of the sheet.

Let the sinusoidal time-varying magnetic field be perpendicular to the area formed by 𝞃 and h.

The varying magnetic field perpendicular to the area formed by 𝞃 and h is;

B= B_maxSinωt

Let us consider a small elemental closed loop path PQRSP of thickness dx, and the distance of the small element from the origin is x. The voltage will be induced in this close loop similar to as induced in a single-turn coil.

Area of the loop PQRS(A)  = 2hx   ——-(1)
Theflux density B = Φ/A

The flux crossing the loop PQRSP =
Φ= BA
Φ= B_maxSinωt2hx        ——————-(2)

RMS voltage induced in the loop 

E=  4.44 f _Φmax 

E= √2Π f Φmax            [√2Π=4.44]
E=√2 Π f Bmax A

E=  √2Π f B_max² hx   ——————-(3)

Resistance of the eddy current path

R = ρ * ( 2h+4x)/ L dx     ————–(4)

The eddy current loss(dP) in a small elemental loop dx
dP = E²/R

dP = E² Ldx/[ρ * ( 2h+4x)]     ——–(5)

Since the thickness of the sheet is much less compared to the height of the sheet, the x dimension can be ignored.

dP = E² Ldx/(ρ*2h)

dP = [√2ΠfB_max2hx]² Ldx/(ρ*2h)]

dP = [4ΠfB_max2hx]² Ldx/(ρ*2h)]

dP = ^{4Π2Bmax2f2hL/ρ       ———-(6)}

Eddy Current Loss per Unit Volume – Formula

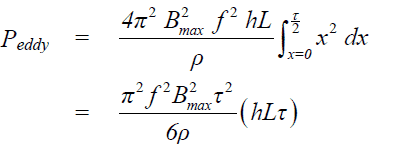
Total eddy current loss =

Eddy current loss per unit volume =

P_eddy = Π²Bmax²f ²𝞃²/ ^{_6ρ——–(7)}

P_eddy= K_e f² Bmax²𝞃^{2   —————(8)}

^Where,

K_{e =} Π²/6ρ

K_e is called the eddy current coefficient.

Key Factors Affecting Eddy Current Loss

Thus the eddy current loss per unit volume is ;

• Proportional to the square of the frequency
• Proportional to the square of the flux density
• Proportional to the square of the thickness of the laminated sheet
• Inversely proportional to the resistivity of the material

Ways to Minimize Eddy Current Loss in Transformers

The eddy current loss depends on the thickness of the steel core. The thin laminated sheet can be used instead of one solid piece of a steel core. The eddy current loss in the steel core is minimized when electrically insulated thin laminated steel sheets are used.

The thin laminated sheet has higher resistance. Therefore, less voltage is induced in the sheet when placed under varying magnetic fields. The low induced voltage with a thin sheet leads to a lower eddy current, and as a result, the heat loss(I²R) is reduced in the thin laminated sheet.

The other electrical quantity that affects the eddy current loss is the ratio of the voltage and frequency. If the following electrical quantities remain constant, the eddy current loss will remain constant.

• Voltage
• Frequency

If the voltage and frequency are constant, the flux density will remain constant because it is proportional to the ratio of V/f.

Practical Applications of Eddy Currents

Eddy current is undesirable in the motor transformer as it causes heat loss, which wastes energy. However, eddy current can be useful in the following applications.

• Damping:  The measuring instrument’s coil is mounted in a light metal frame. When the coil and the pointer rotate in the permanent magnetic field, an eddy current is induced in the metal frame, producing the damping torque.
• Electric Brakes: When a stationary magnetic field is applied to a rotating drum, the eddy current set up in the drum produces the braking torque. The brakes are known as eddy current brakes.
• Induction Furnace: In an induction furnace, the metal to be heated up is placed in the rapidly changing magnetic field produced by a high-frequency current. The eddy current is set up in the metal piece, and thus, the metal gets heated up. The induction-bearing heater also functions on the same principle.
• The effect of eddy current provides braking torque in induction-type energy meters.
• Eddy current instruments are used to detect cracks in metal parts.

Related Articles:

1. No Load Losses in Transformer
2. Why is the core of a power transformer grounded?
3. What is Eddy Current Loss?-Definition and Expression
4. Copper Loss in Transformer – Explanation, Formula & Reduction
5. No Load Losses of Transformer – Formula & Core Loss
6. Types of Losses in a Transformer
7. What is Transformer Core? Construction, Working & Losses